見かけは凄そうに見えても中身は単純ということが人間の世界では間々あるが、数学の
世界でもそういう虚仮威しの問題は多数存在する。
関数
のグラフを描け。
一見すると、
エッ!分数関数! 三角関数も入っている...グラフを描け、じゃ、微分か! 面倒そうやな〜!
ときそうであるが、次のように計算してみると、意外に単純な関数であることが分かる。
三角関数の加法定理を用いて、
この関数 F(x) は、次の問題において出現する。
半径 r の円 O において、直径 AB の上半円部分を弦 PQ が動く。弦 PQ の中点
を M とし、2点 P、Q から直径に下ろした垂線の足をそれぞれ P’、Q’ とおく。
このとき、弦 PQ がどのようであっても常に △MP’Q’ は相似になることを示せ。
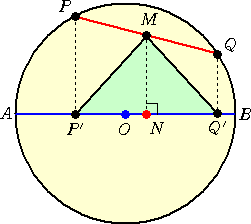
上図において、 ∠BOQ= x 、 ∠POQ=2a とおくと、
P’Q’=r・cos x −r・cos(x+2a)=−r(cos(x+2a)−cos x )
点 M から直径 AB に下ろした垂線の足を N とおくと、中点連結の定理より、
MN=(PP’+QQ’)/2={r・sin x +r・sin(x+2a)}/2=r{sin(x+2a)+sin x }/2
したがって、
となる。 上記の事実から、右辺は弦を見込む角のみに依存する定数で、MN/P’Q’は一
定と言える。△MP’Q’が二等辺三角形であることは明らかなので、このことから、
弦 PQ がどのようであっても常に △MP’Q’ は相似になる
ことが示された。
もっとも、この問題に対しては、次のようなエレガントな解法が知られている。

左図のように、△PQRを考えると、中点連結
の定理から、MP’ ‖ QR となるので、
∠PP’M=∠PRQ=(一定)
となる。すなわち、 ∠MP’Q’は一定。
△MP’Q’は二等辺三角形なので、よって、
常に、△MP’Q’は相似となる。
(コメント) とても感動的な解法ですね!でも、関数 F(x) にも捨てがたい味があるかな?
(参考文献 : ローレン・C・ラーソン 著 秋山 仁 ・ 飯田博和 訳
数学発想ゼミナール 1 (シュプリンガー・フェアラーク東京))
