最初の内はゆっくり増加するのに急にその姿を一変させて人々を驚かす代表は、指数
関数だろう。通常この指数関数は現行学習指導要領では、高校2年で学ぶ「数学Ⅱ」で扱
われるが、昨今の傾向として、「数学Ⅱ」を学ばずに高校を卒業してしまう生徒も増えてき
ている。
(国立教育政策研究所の教育課程実施状況調査(H14)によれば、数学Ⅱの履修率は、87.4%らしい。)
ただ、世の中の急激な変化に対応するためには、指数関数的な概念の熟成も必要と考
えられるので、このことは非常に残念なことである
曽呂利新左衛門が、豊臣秀吉に褒美として次のように要求した話は有名だろう。私自身
小学生時代に、雑誌の付録か何かで読んだ覚えがある。
今日は1粒、明日は2粒で結構。毎日その前の日の2倍の米粒をいただきたい。
最初の内は、
1 、 2 、 4 、 8 、 16 、 32 、 64 、 128 、 ・・・・
と微々たる変化なので大したことがないと思ってしまうが、これを30日間もらい続けると、
1 + 2 + 4 + ・・・ + 229 = 230-1 = 1,073,741,823 (粒)
という莫大な量になってしまう。
約6千粒が1合(1合は大人1食分)で、大人一人が1年間に消費する米の量は1000合
くらいなので、これはおよそ179年分の米の量に匹敵する。
(1合は約150gで、今の世の大人の米消費量が年間で60kgということを考えると、これは400合くらいに
なる。この数字を当てはめると、447年分の米の量に匹敵する。)
この結果を知った豊臣秀吉は、曽呂利新左衛門に褒美を変えてくれるように懇願したそ
うである。
米の量を量る単位として、「石」がある。1石とは、大人一人が年間に消費する米の量で
ある。したがって、1石は大体1000合くらい。
10合が1升で、10升が1斗、4斗が1俵なので、1俵は、400合。 よって、1石当たり、
2.5俵の計算になる。
加賀百万石ということは、米の量に換算すると、250万俵に相当し、約百万人の大人を
養う能力があるということで、加賀藩の大きさがこれで実感できる。
その当時(1598年)の全国検地石高は、1860万石で、豊臣秀吉の受け取る分は、約
12%の223万石だったらしい。
44日間もらい続けると、293万石になったので、豊臣秀吉が青ざめたのも頷ける。
アメリカには、もっと怖ろしい話がある。
ある金持ちが自分の財産がいくらあるかを少女に数えさせ、少女は、褒美として次のよう
に要求した。
初日は2セント、毎日前の日の金額の2乗をいただく。6日間の支払いでいい。
これこそ正に悪魔のささやきだろう。「初日は2セント」「6日間だけ」という心地よい響きに
「前の日の2乗」がどんな顛末になってしまうのか見えなくなってしまう。
金持ちは財産のすべてを少女に明け渡すことになってしまったそうである。
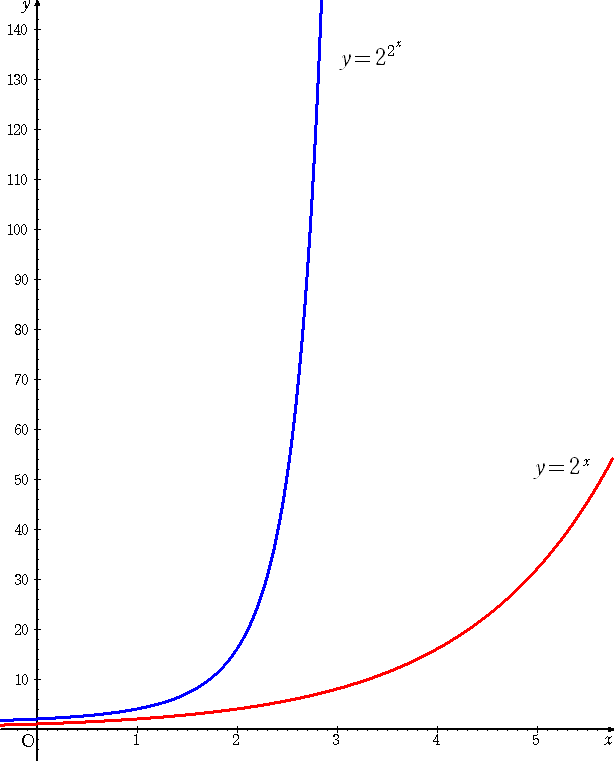
下図は、上記で登場した関数のグラフである。この2つのグラフを比較すると、アメリカの
少女のえげつなさが実感できることだろう。
(参考文献 中村和幸 著 就職試験の数学 (講談社))
