次は、平成19年度 成蹊中学入試問題を改題したものである。この問題文には、深遠
なる性質が隠れている。その性質を看破したときの驚きは、筆舌に尽くしがたい。
このような良問が中学校入試で問われていることに安堵するとともに、この問題を作問し
た方に敬意を表したい。
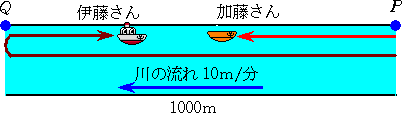
加藤さんは、小舟に乗って、分速10mの川の流れに身を任せ、のんびりと地点P
から下流の地点Qまでの1000mの川下りを楽しんでいる。遊び心十分な伊藤さん
は、モーターボートに乗って加藤さんと同時に地点Pを出発し、地点Qに着いて直ぐ
引き返し、地点Pの出発から40分後に加藤さんの小舟に出会った。
このとき、川の流れが静止しているときのモーターボートの分速 V(m/分)を求め
よ。
この問題に対して当初私が用意した解答は下記のようなものである。
(解) 40分間に加藤さんは、40×10=400(m)下っているので、地点Qの上流 600m
の地点で、伊藤さんと出会う。
したがって、次の等式が成り立つ。
これを解いて、 V=40(m/分) (終)
しかしながら、答えは出るものの、解法に用いている手法は全く小学生的ではない。上記
の問題はあくまでも小学生が対象なので、上記の解法は不適切なものと判断される。
それでは、小学生向きの解法はどんなものだろうか?入試選抜の作業の合間に、この問
いかけを今日1日ずっと考えていた。
いろいろ計算しているとき、次の驚くべき性質に気がついた。すなわち、
伊藤さんが地点Pから地点Qまでに要する時間と地点Qで折り返してから加藤さん
に出会うまでに要する時間は相等しい
当初信じられない結果であったが、次のような計算結果から確かに上記の性質の成り立
つことが了解される。
伊藤さんが地点Pから地点Qまでに要する時間を T、地点Qで折り返してから加藤さんに
出会うまでに要する時間を T’ とすると、
(V+10)×T=(V−10)×T’+10×40 、 T+T’=40
よって、 VT+10T=VT’−10T’+400 より、
VT=VT’−10(T+T’)+400=VT’−10×40+400=VT’
したがって、 T=T’ となる。
この性質に気がつけば、上記の問題は次のように軽妙に解かれうる。
(解) 伊藤さんが地点Pから地点Qまでに要する時間は、 40÷2=20(分)なので、
伊藤さんのモーターボートの下りの速さは、 1000÷20=50(m/分) である。
よって、川の流れが静止しているときのモーターボートの速さは、
50−10=40(m/分)
となる。 (終)
(コメント) この性質は、小学校の算数レベルでは常識なのだろうか?とても常識である
ようには思えないのだが...。解答は算数レベルだが、考え方は高校レベル
のような...予感!
以前テレビか何かのクイズ番組で、「伊藤さんが加藤さんに出会ったお店の名前は?」
というのがあった。もちろん答えは、「イトーヨーカドー」である。なぜなら、
「伊藤〜!」 、 「ヨ〜、加藤!」
だから。(分かってもらえたかな?)
(追記) 平成20年2月9日付け
有楽町マリオンで第1回朝日杯将棋オープン戦の公開対局を観戦しながら、羽生二冠−
丸山九段、行方八段−阿久津六段というゴールデンカードにも関わらず、頭の半分は上記
の問題を考えていた。上記の計算が全く小学生的でなかったからだ。
伊藤さんが地点Pを出発して地点Qに到達したときの加藤さんの位置をRとする。
このとき、明らかに、
伊藤さんが進んだ距離(地点P〜地点Q)から加藤さんが進んだ距離(地点P〜地点R)
を引いたもの、即ち、地点Q〜地点Rの距離
と、
伊藤さんが地点Qで折り返して加藤さんに出会うまでに進んだ距離に加藤さんが進ん
だ距離(地点R〜伊藤さんに出会う地点)を足したもの、即ち、地点Q〜地点Rの距離
は相等しい。
地点Qで折り返す前の伊藤さんの加藤さんに対する相対速度は、(V+10)−10=V で、
折り返した後の伊藤さんの加藤さんに対する相対速度は、(V−10)−(−10)=V である。
以上から、同一の区間(地点Q〜地点R)において、両者の速さが同じなので、かかる時
間も等しい。
このように考えると、小学生にも十分耐えうる問題となったのかな...? あっ、「相対速
度」という考えが小学生には厳しいかも...(^^;)。
