丂暯惉俀侽擭搙偺戝妛擖帋僙儞僞乕帋尡偑丄侾寧侾俋擔乮搚乯乣俀侽擔乮擔乯偵峴傢傟傞丅悢妛
嘥偺帋尡偼丄戞俀擔偱偁傞丅
丂俀師娭悢偱偼丄師偺傛偆側栤戣偑昿弌偱偁傞丅
栤戣丂丂倎 傪掕悢偲偟丄俀師娭悢 倷亖俀倶2亅係倎倶亄俁丂傪峫偊傞丅丂倶 偑丄亅侾亝倶亝侾
丂丂丂丂偺斖埻偵偁傞偲偒丄偙偺俀師娭悢偺嵟戝抣 俵乮倎乯丄嵟彫抣 倣乮倎乯 傪偦傟偧傟
丂丂丂丂媮傔傛丅
丂偙偺栤戣偼丄幉偺埵抲偱応崌暘偗偡傞偙偲偑億僀儞僩偱偁傞丅
乮夝乯丂俥乮倶乯亖俀倶2亅係倎倶亄俁亖俀乮倶亅倎乯2亄俁亅俀倎2丂傛傝丄幉偺幃偼丄丂倶亖倎
丂傑偢丄嵟戝抣傪媮傔傞丅
丂丂丂
 丂丂丂丂丂丂
丂丂丂丂丂丂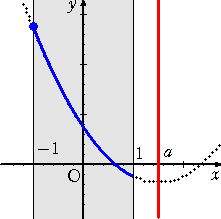
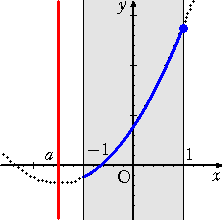
丂忋恾偐傜丄丂倎亙侽丂偺偲偒丄丂丂俵乮倎乯亖俥乮侾乯亖俆亅係倎
丂丂丂丂丂丂丂丂倎亞侽丂偺偲偒丄丂丂俵乮倎乯亖俥乮亅侾乯亖俆亄係倎
丂師偵丄嵟彫抣傪媮傔傞丅
 丂丂
丂丂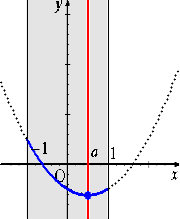 丂丂
丂丂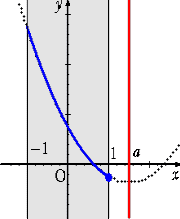
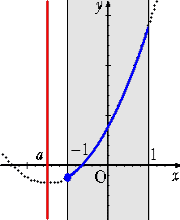
丂忋恾偐傜丄丂倎亙亅侾丂偺偲偒丄丂丂倣乮倎乯亖俥乮亅侾乯亖俆亄係倎
丂丂丂丂丂丂丂丂亅侾亝倎亝侾丂偺偲偒丄丂丂倣乮倎乯亖俥乮倎乯亖俁亅俀倎2
丂丂丂丂丂丂丂丂倎亜侾丂偺偲偒丄丂丂倣乮倎乯亖俥乮侾乯亖俆亅係倎丂丂乮廔乯
丂忋婰偺栤戣偱偼暥帤偑娭悢幃偵擖偭偰偄傞偑丄掕媊堟偺曽偵擖傞応崌傕偁傞丅
栤戣丂丂倎 傪掕悢偲偟丄俀師娭悢 倷亖俀倶2亅係倶亄俁丂傪峫偊傞丅丂倶 偑丄倎亝倶亝倎亄侾
丂丂丂丂偺斖埻偵偁傞偲偒丄偙偺俀師娭悢偺嵟戝抣 俵乮倎乯丄嵟彫抣 倣乮倎乯 傪偦傟偧傟
丂丂丂丂媮傔傛丅
丂偙偺栤戣偵懳偟偰偼丄捠忢師偺傛偆偵夝偐傟傞偙偲偑懡偄偩傠偆丅
乮夝乯丂丂俥乮倶乯亖俀倶2亅係倶亄俁亖俀乮倶亅侾乯2亄侾丂傛傝丄幉偺幃偼丄丂倶亖侾
丂丂丂嬫娫 倎亝倶亝倎亄侾 偺暆偼丄侾偱偁傞丅
丂傑偢丄嵟戝抣傪媮傔傞丅丂俥乮倎乯亖俥乮倎亄侾乯丂偲側傞偺偼柧傜偐偵丄倎亖侾/俀丂偺偲偒偱偁傞丅
丂丂丂丂丂
 丂丂丂丂丂丂丂
丂丂丂丂丂丂丂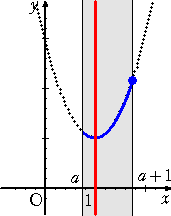
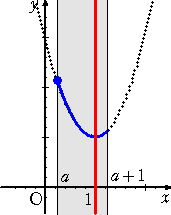
丂忋恾偐傜丄丂倎亙侾/俀丂偺偲偒丄丂丂俵乮倎乯亖俥乮倎乯亖俀乮倎亅侾乯2亄侾
丂丂丂丂丂丂丂丂倎亞侾/俀丂偺偲偒丄丂丂俵乮倎乯亖俥乮倎亄侾乯亖俀倎2亄侾
丂師偵丄嵟彫抣傪媮傔傞丅
 丂丂丂
丂丂丂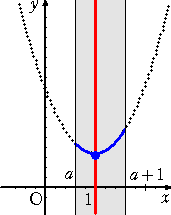 丂丂丂
丂丂丂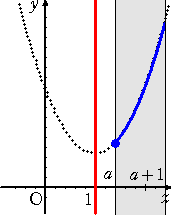
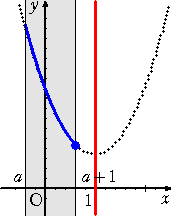
丂忋恾偐傜丄丂倎亙侽丂偺偲偒丄丂丂倣乮倎乯亖俥乮倎亄侾乯亖俀倎2亄侾
丂丂丂丂丂丂丂丂侽亝倎亝侾丂偺偲偒丄丂丂倣乮倎乯亖俥乮侾乯亖侾
丂丂丂丂丂丂丂丂倎亜侾丂偺偲偒丄丂丂倣乮倎乯亖俥乮倎乯亖俀乮倎亅侾乯2亄侾丂丂乮廔乯
丂偙偺俀偮偺栤戣偺夝朄傪斾妑偡傞偲偒丄慜幰偺曽偑峫偊傗偡偄偩傠偆丅偟偐偟丄師偺傛偆偵
峫偊傟偽丄屻幰偺栤戣傕慜幰偲摨條偵峫偊傞偙偲偑弌棃傞丅俀偮偺栤戣偼摨偠僷僞乕儞偺栤
戣偱偁傞偲偄偆偙偲偑巉偊傞丅
丂屻幰偺栤戣傪慜幰偺夝朄僷僞乕儞偱夝偔僐僣偼丄掕悢乽倎乿傪屌掕偡傞偙偲偱偁傞丅
乮暿夝乯丂俥乮倶乯亖俀倶2亅係倶亄俁亖俀乮倶亅侾乯2亄侾丂傛傝丄幉偺幃偼丄丂倶亖侾
丂丂丂嬫娫 倎亝倶亝倎亄侾 偺暆偼丄侾偱偁傞丅傛偭偰丄嬫娫偺拞墰抣偼丄倎亄侾/俀
丂傑偢丄嵟戝抣傪媮傔傞丅
丂丂丂丂丂
 丂丂丂丂丂丂丂
丂丂丂丂丂丂丂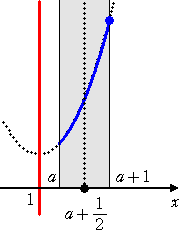
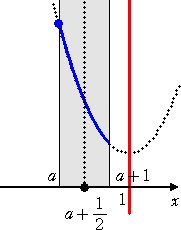
丂忋恾偐傜丄
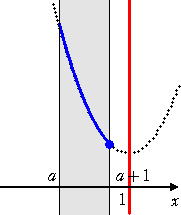
丂丂丂倎亄侾/俀亙侾丂偡側傢偪丄丂倎亙侾/俀丂偺偲偒丄丂丂俵乮倎乯亖俥乮倎乯亖俀乮倎亅侾乯2亄侾
丂丂丂倎亄侾/俀亞侾丂偡側傢偪丄丂倎亞侾/俀丂偺偲偒丄丂丂俵乮倎乯亖俥乮倎亄侾乯亖俀倎2亄侾
丂師偵丄嵟彫抣傪媮傔傞丅
 丂丂丂
丂丂丂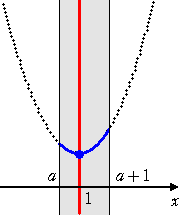 丂丂丂
丂丂丂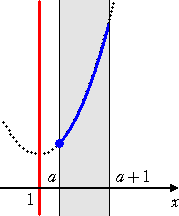
丂忋恾偐傜丄丂倎亄侾亙侾丂偡側傢偪丄丂倎亙侽丂偺偲偒丄丂丂倣乮倎乯亖俥乮倎亄侾乯亖俀倎2亄侾
丂丂丂丂丂丂丂丂倎亝侾亝倎亄侾丂偡側傢偪丄丂侽亝倎亝侾丂偺偲偒丄丂丂倣乮倎乯亖俥乮侾乯亖侾
丂丂丂丂丂丂丂丂倎亜侾丂偺偲偒丄丂丂倣乮倎乯亖俥乮倎乯亖俀乮倎亅侾乯2亄侾丂丂乮廔乯
乮僐儊儞僩乯丂崱傑偱丄俀條偵夝偄偰偒偨栤戣偑幚偼摨偠夝朄偱夝偗傞偲偼嬃偒偱偡両偙偺傛
丂丂丂丂丂丂偆側擣幆偑丄栤戣傪峫偊傞忋偱偲偰傕戝愗偱偡傛両偲偄偆偙偲傪壨崌弇偺愭惗傛
丂丂丂丂丂丂傝嫵傢傝傑偟偨丅傑偝偵丄乽梊旛峑丄嫲傞傋偟両乿偱偡偹丏丏丏丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
