自然数 ｎ の階乗 ｎ！ について、次のような性質があることは興味深い。
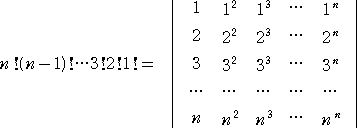
この表現の使い道は？と問われれば答に窮してしまうほど、その意義は怪しいが、形自
体には他を寄せ付けない美しさがある。
例 ｎ＝３ のときについて確認してみよう。
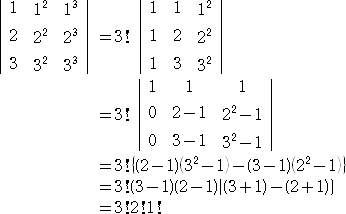
となる。 この計算の中で、
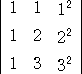
の形をした行列式は、有名な行列式である。
一般に、
の形をした行列式は、Ｖａｎ ｄｅｒ Ｍｏｎｄｅ （ファンデルモンデ）の行列式と言われる。
この行列式の値は、簡単な計算から、
となることが分かる。
実際に、任意の ｉ 、ｊ について、ｘｉ＝ｘｊ とすると、行列式の性質から、０ となるので、
与えられた行列式は、ｘｉ−ｘｊ （ ｉ ＜ ｊ ）で割り切れる。
よって、与えられた行列式は、
（ ｋ は実数の定数） とおける。ここで、左辺における ｘ2ｘ32ｘ43・・・ｘｎｎ-1 の係数は明らかに、１ であり、
右辺における ｘ2ｘ32ｘ43・・・ｘｎｎ-1 の係数は、
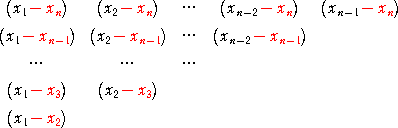
の形を考慮して、 ｋ（−１）（−１）2（−１）3・・・（−１）ｎ-1＝
となる。よって、
となり、上記の公式が示された。この公式を用いると、上記の例の問題は、次のように解かれる。
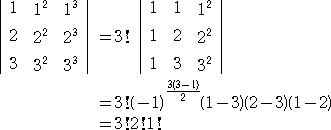
同様にして、冒頭の等式も示される。
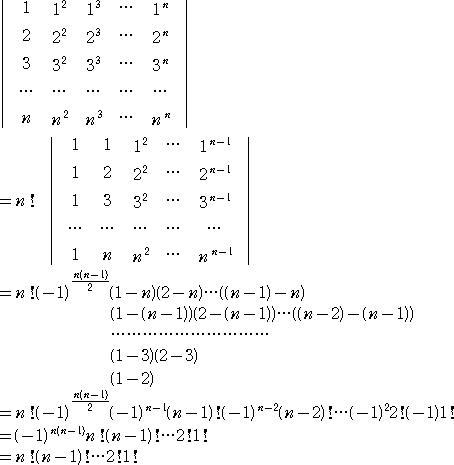
当ＨＰの掲示板「出会いの泉」に、平成２０年１０月２６日付けで、ＨＮ「凡人」さんが下記の
ように書き込まれた。
階乗の意外な表現の一般における証明ですが、ファンデルモンデの行列式を利用すれ
ば簡単に証明出来ると思います。しかし、実は一昨年受験した第１２５回実用数学技能検
定１級に似たような問題があったのですが、「ファンデルモンデの行列式から（以下略）」と
解答したところ恐らく誤答となっている様だったので、怪しい所もありますが。（採点された
解答用紙は返却されないので、得点からの類推ですが、誤答となっているのはこの問題
だと思います）
数検の問題はこの場に載せても良いものか迷う所なのでやめときます。
確かに、ファンデルモンデの行列式を利用すれば簡単に証明されますね！でも問題自体
が、ファンデルモンデの行列式とほとんど同じような．．．予感。数検１級の問題がどんな問
題か大いに興味がありますが、閲覧は無理ですよね。
当初は、証明が面倒そうだったので敬遠していましたが、「凡人」さんの声に後押しされて
証明に挑戦してみました。この機会を与えていただいた「凡人」さんに感謝いたします。
