・ バドミントン S.H氏
1999年にバレーボール競技で、「サイドアウト制」から「ラリーポイント制」が新たに採用
された。自らのミス毎に相手方の得点になるこの制度は、試合時間の短縮という効果以外
に1点1点の重みから生ずる緊張感、集中力のアップが選手達に課せられるという側面も
持つ。
この制度が、2006年度からバドミントン競技でも採用され、普及している。
バレーボールの場合は「ローテーション」があり、誰が次のサーブを打つのか素人目でも
明らかだが、バドミントンの場合は、選手がコート内を縦横無尽に走り回り、時々素人であ
る私は考え込んでしまうこともある。
しかし、選手達は、現在のスコアから瞬時に誰がどこからサーブするのかを見いだし、試
合は滞りなく進行する。これなど、端から見ていて思わず感動してしまう。
バドミントンにおいて、サーブを打つ順番、場所は明確にそのルールに定められている。
シングルスもあるが、ダブルスに限定して話を進めよう。
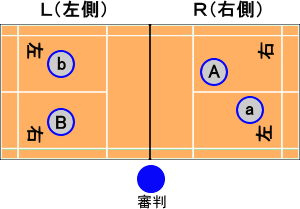
上図は、(A,a)チームと(B,b)チームの対戦で、(A,a)チームがサーブ権を持っている
ときの試合開始の状況である。
バドミントンにおいて、サーブおよびレシーブの方法は下記のようになっている。
(1) サーブする側のスコアが「0」か「偶数」のときは、コート右から、「奇数」のとき
はコート左からサービスをする。
(2) サーブした側がラリーに勝った場合は、同一サーバーが左右のサービスコート
を替えてサービスをする。
レシーブした側がラリーに勝った場合は、サービスオーバー(Serviceover)
となってサービス権が移る。サービス権を得たときのスコアが、「偶数」のときは
コート右から、「奇数」のときはコート左からその位置にいる者がサービスをする。
(3) サービスする順番は、上図だと、 A→b→a→B となる。サービス権が戻って
きたときは、前回と異なる者がサービスする。
どんなときも、サービス側のスコアが「偶数」なら「右」、「奇数」なら「左」と決まっていたん
ですね!
今、試合が進行して下記のようなスコアになったものとする。
| A |
S |
0 |
1 |
|
|
|
|
|
5 |
|
|
|
|
|
7 |
|
|
|
|
| a |
|
|
|
|
2 |
3 |
4 |
|
|
|
|
6 |
|
|
|
|
|
|
|
| B |
R |
0 |
|
|
|
|
|
2 |
|
|
|
|
5 |
6 |
|
|
|
|
|
| b |
|
|
|
1 |
|
|
|
|
|
3 |
4 |
|
|
|
|
|
|
|
|
<試合経過> Aがサービスして1点を得たが次のサービスを失敗してサービス権が移動
し、相手側に1点が入る。1点という奇数の点数なので、コート左のbが次に
サービスした。が、失敗。サービス権が移動し、相手側に1点が入り、合計
点数が2点となる。偶数の点数なので、コート右のaが次にサービスする。
2本続けて得点を得たが、3本目を失敗。サービス権が移動し、相手側に
1点が入り、合計点数が2点となる。偶数の点数なので、コート右のBが次
にサービスするが失敗。サービス権が移動し、相手側に1点が入り、合計
点数が5点となる。奇数の点数なので、コート左のAが次にサービスした。
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
上記のスコア表は、いろいろな情報の宝庫である。例えば、サービスの順番が、
A → b → a → B → A → b → a → B → A → ・・・・・・
と変わっていくことが見て取れる。
さて、そこで問題です。
Bがサービスに失敗して(A,a)チームが7点を得たとき、
コート内で、 A , a , B , b の4人の配置はどうなっているだろうか?
バドミントンに詳しい方なら当たり前かな?下図のような配置になっている筈。
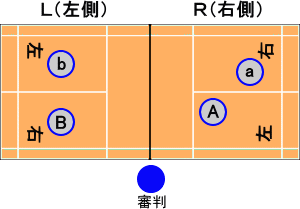
実は、この配置は直近のスコア(7−6)から直ちに求められる。
(試合の最初から順次考えても矛盾しないところに驚かされる。)
Bの次にサービスするのはAだが、自分たちのスコアが奇数の7点なので、コート左にい
る。また、相手のスコアが偶数の6点なので、コート右にBがいることになる。
何となく数学の匂いがするような、そんな雰囲気だ!分かりにくい競技規則もそう考えれ
ば、苦痛でなくなるかも...?
ところで、バドミントンに限らない話題になるが、トーナメントにおけるシードの配置も、とて
も数学的に感じる。
例えば、16チームのトーナメントを考える。試合数は全部で、 16−1=15 である。
16チームに明確に序列がついている場合、下図のように配置するのが平等らしい。
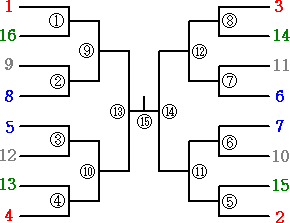
(丸数字は、試合の順番)
対戦チームの実力の順位で、ちょうど、「和が一定」という原則が貫かれていて面白い。
ただ、シード権「1」のチームが他のチームに比べて絶対的に楽な試合ばかりであること
が若干気になる。気のせいだろうか?




