ギリシアの三大作図不可能問題と言えば、
（１） 円 積 問 題 ・・・ 円と等しい面積をもつ正方形を作ること
（２） 立方体倍積問題 ・・・ 立方体の体積の２倍に等しい体積の立方体を作ること
（３） 角の三等分問題 ・・・ 任意の角を３等分すること
が有名である。
何れも定規とコンパスによって作図することは不可能であることが示されている。
（（１）は「円周率が超越数」（1882年 リンデマン）から、（２）（３）はワンツェル（1837年）による）
このうちの（１） 円 積 問 題 について、秋山 仁 先生が、
定規とコンパスのみでは作図不可能だが、「円を転がす」ことを認めれば作図は可能
ということを、
NHK高校講座 数学基礎 「ピタゴラスの定理（２） 応用と発展」 （平成１９年７月１９日放送）
で講義されていた。 「エッ！」と思わず画面に引き込まれたというのが率直な感想だ。
次のように作図するらしい。
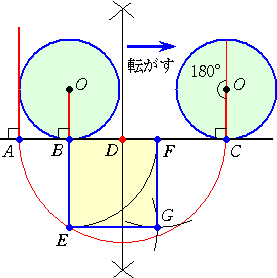半径 ｒ の円 Ｏ が半周分だけ転がり水平線との接点を左図のように Ｂ 、 Ｃ とする。
ただし、AB ＝ ｒ である。
線分 ＡＣ の中点を Ｄ とし、Ｄ を中心とし
半径 ＡＤ の半円を描く。
その半円と直線 ＯＢ との交点を Ｅ とする。
このとき、正方形 ＢＥＧＦ が求めるもので
ある。
実際に、 ＢＣ＝πｒ より、 ＡＤ＝ＤＥ＝ＤＣ＝（π＋１）ｒ/２
ＢＤ＝（π＋１）ｒ/２−ｒ＝（π−１）ｒ/２
よって、 ＢＥ2＝｛（π＋１）ｒ/２｝2−｛（π−１）ｒ/２｝2＝πｒ2 となり、
円 Ｏ の面積と正方形 ＢＥＧＦ の面積は等しい。
（コメント） 動的に「転がす」ということが、如何に高度な技であるかが実感できました。
