・　正三角形を作る 　　　 　　　　　　　　　　　　　Ｓ．Ｈ氏

　１辺の長さが２の正方形３個と３辺の長さが２、１、の直角三角形を何個か組み合わ
せて一つの正三角形を作りたい。ただし、直角三角形の個数は少ない方がよい。

　正三角形の１辺の長さを ａ とする。　直角三角形を ｘ 個使うものとすると、次の等式が

成り立つ。
　　　　　　　　　　１２＋（/２）ｘ＝（/４）ａ²

このとき、　　ａ²＝２ｘ＋１６　となる。

　ここで、　ａ＝ｍ＋ｎ　（ｍ、ｎ は自然数）とすると、

　　　　　　　　ｍ²＋３ｎ²＝２ｘ　　、　　２ｍｎ＝１６

　このとき、　ｍｎ＝８　で、　（ ｍ ， ｎ ）＝（ １ ， ８ ）、（ ２ ， ４ ）、（ ４ ， ２ ）、（ ８ ， １ ）

において、順次 ｘ の値は、　なし　、２６　、１４　、なし。

　以上から、　ｘ＝１４　のとき、最も直角三角形の個数が少なく正三角形が作れる（筈！）。

実際に、組み合わせてみると、下図のようになる。

　　　　　　　　


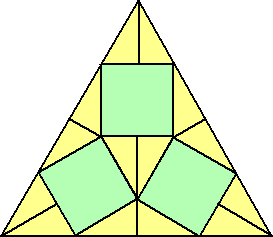
　計算の結果では、これが最小の正三角形のはずだが、もしかしたらもっと別な組合せが
あるかもしれない。ちょっと自信がもてないかな．．．。