・ 英語の試験もなかなか S.H氏
平成19年度大学入試センター試験の英語の問題に、面白い問題が出ているということ
を、当HPがいつもお世話になっている加俊さんから教えていただいた。
(当HP掲示板「出会いの泉」(平成19年2月5日付け))
今年のセンター入試の英語の問題に、面白そうな数学のゲームみたいなのがありました。
二人が交互に行うゲームです。用意するものは、紙と鉛筆のみ。
(1) 始めにいくつかの点を書く。(最初は、3つ、4つのときから考えた方がよい。)
(2) それらのうちの一つから線を引き始め自分または他の線と交わらないように適当な
点と結ぶ。このとき、点は元の点でもよい。
ただし、一つの点から出る線は三本以下とする。
(3) 引いた線上に一つ点を付ける。つまり、このとき新たに作った点は、すでに二本の
線に結ばれていることになる。
(4) (2)~(3)を繰り返し、線が引けなくなったら終了。
かなり長い勝負になりそうですが、必勝法はあるのでしょうか??
英語の試験も「なかなかやる~!」と思いながら、この問いかけに興味を持ったので、少し
考えてみた。ここでは、最後に線を引いた人を、このゲームの勝者とする。
3個の点がある場合
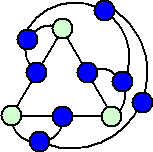
左図のように、8本の線を引けば、後手が勝つことになるわけ
だが、線の引き方はもっと別な場合もあるので、事は、そう単純
にはいかないようだ。
当HPがいつもお世話になっている、らすかるさんによれば、下図のように先手が最初の
1手で他の1点を内部に、残りの1点を外部にあるように自分自身を線で結ぶと先手必勝
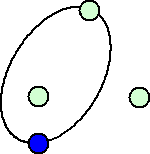
になるそうである。なぜならば、後手の可能性は、
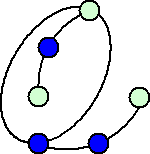
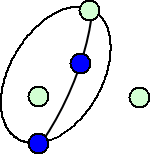

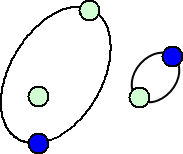
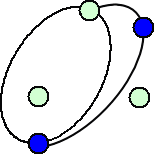
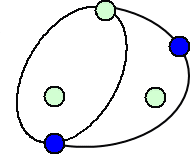
など、いろいろな場合があるが、後手がどのような線を引いても最後の1本を先手が必ず
引けるからである。(上図の続きを是非楽しんで欲しいと思う!)
したがって、3個の点の場合は、
自分自身に戻る線を、他の1点を内部に、残りの点を外部にあるように引く
ことが、先手必勝形に持ち込む最良の方法である。先手必勝形を見つけるには、線の本数
が奇数になる最小のパターンを見つければいいようだ。このことは加俊さんが指摘している。
当HPがいつもお世話になっている未菜実さんからの情報によると、このゲームは、スプラ
ウト(Sprouts)ゲームというようで、次の本が詳しいそうである。
マーチンガードナー 著 一松 信 訳 数学カーニバルⅠ (紀伊国屋書店) 11p~20p
このゲームの発案者は、コンウェイとパターソン(1960年代後半)とのことである。
未菜実さんによれば、必勝法は、点の個数が 1~6個までは分かっているとのことで、
| 点の個数 |
1 |
2 |
3 |
4 |
5 |
6 |
| 必勝者 |
後手 |
後手 |
先手 |
先手 |
先手 |
後手 |
となるそうである。因みに、6個の点の場合の証明は、49ページにも及ぶらしい!
(参考) 未菜実さんからの情報によると、証明は当時、ケンブリッジの数学科のデニス・
P・モリソン(Denis P.Mollison)によるもので、コンウェイが10シリングの賭金を出
したのに対して、証明を提出した、となっていて、文献として残っているかどうか
は不明だそうである。
(追記) 平成19年2月14日付け
らすかるさんのご奮闘により、7個の点の場合が解決されました。
「後手必勝」とのことです。(80時間!かかったそうです...スゴイ。)
らすかるさん、お疲れ様でした! (追記終)
実際に、必勝手順を考察してみよう。
1個の点の場合、後手が必勝であることは明らかだろう。
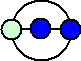
2個の点の場合、後手が必勝であることはそれほど明らかではない。
もし先手が、

ときたら、後手は、
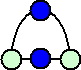
と応対すればよい。このとき、先手がどう線を結んでも後手は必ず勝てる線の引き方がある
ので、後手必勝である。
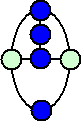
もし先手が、

ときたら、後手は、

と応対すればよい。このとき、先手がどう線を結んでも後手は必ず勝てる線の引き方がある
ので、後手必勝である。

もし先手が、

ときたら、後手は、
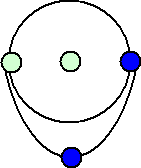
と応対すればよい。このとき、先手がどう線を結んでも後手は必ず勝てる線の引き方がある
ので、後手必勝である。
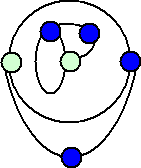
3個の点の場合、先手が必勝であることは比較的容易に確かめられた。しかし、2個の
点での検証からも分かるように、後手必勝を示すのはかなり難しそうだ。
未菜実さんからの情報でも、6個の点の場合、後手必勝を証明するのに、49ページも必
要とのことであるが、2個の場合の経験から予想できる数字である!
4個の点の場合、5個の点の場合も、一応、下図のように線の引き方の一つを書いては
みたものの、ゲームなのでそのようにはすんなりいかないのが玉に瑕...。
| 4個の点がある場合 |
|
5個の点がある場合 |
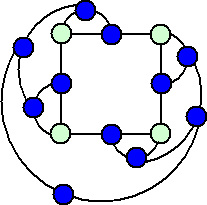 |
|
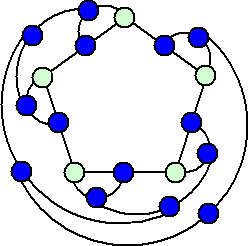 |
両者とも先手必勝ということなので、初手に先手がどういう対応をし、後手の対応に対して
先手がどう答えるのかを考えればいいわけだが、気が遠くなりそうな雰囲気である。
(追記) 平成19年2月14日付け
らすかるさんのご奮闘により、4個、5個の点の場合について、先手が初手
に取るべき手が明らかとなった。
4個の点の場合は、
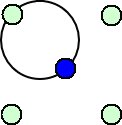
5個の点の場合は、
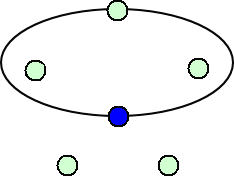
(コメント) この後どう応手するのか、楽しみが増えましたね! (追記終)
(コメント) この問題を原文で英語の先生に見てもらったところ、大変驚かれていました。私
も、まさか英語の問題に数学の問題があるとは思いませんでした。でも、たいそう
な英文を読ませておいて、設問のレベルの低さには驚きました。あれでは英文を
正確に読まなくても正解が書けてしまいますね!配点が12点分あるのに...。
これは、受験生に点をやるための問題なのですかね?
面白い問題をお教えいただいた加俊さんに感謝いたします。
(追記) 未菜実さんからの情報によると、
N個の点に対して、線が引ける最大本数は、3N-1である
ことが、コンウェイによって証明されているそうである。(2月7日付け)
ということは、次の手順で線を引く場合に最大本数が与えられるのだろうか?
(1) トポロジー的に、N個の点は、正N角形の頂点としてよい。隣り合う頂点を結んで辺と
する。 ・・・・ このとき、N本の線が引かれる。
(2) 各辺の中点と隣り合う頂点の一つを結ぶ。 ・・・・ このとき、N本の線が引かれる。
(3) このときできるN個の点から2点を選んで結ぶ。
・・・・ このとき、Nが偶数なら、N/2本の線が引かれる。
・・・・ このとき、Nが奇数なら、(N-1)/2本の線が引かれる。
(4) Nが偶数のとき、N/2個の点について、(3)の操作を行う。
Nが奇数のとき、(N-1)/2+1個の点について、(3)の操作を行う。
以上の操作を繰り返すことにより、任意のN個の点について、描かれる線分の本数が求
められる。(最後の2点を結んだ時点で終了!)
例 N=3 のとき
線の本数=3+3+(3-1)/2+(1+1)/2=8
例 N=4 のとき
線の本数=4+4+4/2+2/2=11
例 N=5 のとき
線の本数=5+5+(5-1)/2+{(2+1)-1}/2+(1+1)/2=14
例 N=6 のとき
線の本数=6+6+6/2+(3-1)/2+(1+1)/2=17
上記の計算は、ガウス記号を用いれば、もっとすっきりするだろう。
上記の(1)~(4)の手順で、(1)(2)は必然で、2N本の線が引かれる。
(3)(4)によって出来る点は、もはやあと1点としか結ぶことができず、また、2つの点から
同じ性質をもつ点を1つ生成しているので、できる線の本数は、
[N/2]+[(N-[N/2])/2]+・・・・・=N-1
である。以上から、N個の点に対して、結ばれる線の本数は、
N+N+N-1 = 3N-1
となる。
先手・後手が勝負を終わらせまいと互いに譲歩しつつ線を引いた場合の最大本数が、
(点の個数)×(1点から出る線の最大数)-1
の形をしている点がとても興味深い。
ところで、
N個の点があるとき、引くことが出来る線の最大本数は、3N-1本
ということを、らすかるさんは、「ほとんど自明!」(H19.2.7)と仰っている。
らすかるさんが使っている文言をちょっと修正させていただいて、一応検証しておこう。
N個の点があるとする。1個の点から3本まで線が引けるので、1個の点には3つの接合
部があると考えられる。よって、N個の点全体では、接合部の合計は、3N個ある。
点と点(自分自身を含む)を線で結ぶということは、3N個の接合部から2つを選んで結ぶ
ということである。この際、新たに1点が生じ、接合部が1個だけ増える。
このことから、線を1本引くことにより、接合部の個数は、2減1増なので、結局、1個だけ
減少する。
したがって、接合部の個数が3N個から1個になるまで、線を引くことが可能で、よって、
引くことが出来る線の最大本数は、3N-1本である。
 らすかるさんによれば、
らすかるさんによれば、
「閉領域によって孤立箇所が出来ると、3N-1
本より減り、ここがゲームになっている。
閉領域で孤立箇所が出来ないように隣接点ば
かり繋いでいけば、必ず 3N-1 本になる。」
(左図は、N=5 で、線の本数が、14本の場合)
上記では、線を引くことが出来る最大本数が「3N-1本」ということであったが、らすかる
さんは、「3N-1本」が必ず可能であることを次のように証明された。(H19年2月8日付け)
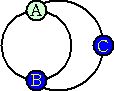
最初に適当な点Aを選び、1本目の線はAからAのループとし、中間点をBとする。2本目
の線は、AとBを上記ループの外側で結び、中間点をCとする。これで、点Aと繋がっている
図形から出せる線は残り1本(Cから)だけとなり、他の新しい点を使わないと線が引けない
状態になる。(以上の線はすべて閉領域に他の点を含まないようにAの近傍で引く)
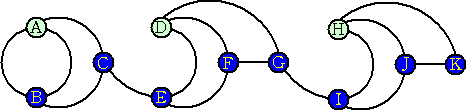
次に新しい点Dを選び、1本目の線はCとDを結び、中間点をEとする。2本目はDとEを結
び、中間点をFとする。3本目はDとFを、閉ループD-E-F-Dの外側で結び、中間点をG
とする。これで点Aと繋がっている図形から出せる線は残り1本(Gから)だけとなり、他の新
しい点を使わないと線が引けない状態になる。(以上の線も、他の点を閉領域内に含まない
ようにCからDを結んだ線の近傍で引く)
この操作を繰り返すと、Aの近傍-Dの近傍-3つ目の新しい点の近傍-…と数珠繋ぎの
図形が出来るが、他の新しい点を閉領域に閉じ込めることがないので、残りの新しい点が
使用出来なくなることはない。
よって、点Aを使って、2本、次に新しい点を使うたびに3本多く線が引けるので、3N-1本
の線を引くことが可能である。
らすかるさんの証明に対して、当HPがいつもお世話になっている加俊さんは、
N個の点があるとき、引くことが出来る線の最大本数は、3N-1本
ということを、次のように不等式を用いて証明された。(平成19年2月8日付け)
最初の点の個数が、N 個のときに引ける線の最大本数を、F(N) と表す。
明らかに、N=1 のとき、 F(1)=2 である。
次に N≧2 とする。N個の各点において、自分自身と線で結び、さらに、そのとき出来る
点と自分自身をループの外部で結ぶ。このとき、あと1本しか線が引けない点が1個できる。
これらの点は全部でN個ある。このうち2個を選んで線で結び、このとき出来る点と残りの
N-2個の点から1個選んだ点を結ぶ。
この操作を続けると、全部でN-1本の線を引くことが出来る。
よって、 F(N)≧2N+N-1≧3N-1
ところで、1本の点からは、3本の線以下しか引けず、1本線を引く毎に、点から出せる線の
総数が1減っていくことから、 F(N)≦3N-1
したがって、 F(N)=3N-1 である。
(コメント) やっと、追いついたかな...?
当HPがいつもお世話になっているHN「FN」さんからの問題提起です。
(平成22年11月19日付け)
上記では、最初の点が N 個であるとして、次のことが示されている。
引ける線の数、即ち、勝負がつくまでの手数は、3N-1 以下である。
(実際に、3N-1本の線が引けるケースがある!)
従って、勝負がつくまでの手数の最大値は、3N-1であることは証明されています。
では、
勝負がつくまでの手数の最小値、即ち、引ける線の数の最小値
はどうなるでしょうか?
攻略法さんの考察によれば、答えは「2N」とのことである。(平成22年11月24日付け)
考 察(証明ではありません!)
最初の点を、A、B、C、・・・ とし、追加される点を順に、1、2、3、・・・ とする。
N=3 の場合
ABC12345678
0手:00000000000
1手:20020000000
2手:22022000000
3手:33022200000
4手:33222220000
5手:33332222000
6手:33333322200 ←
7手:33333333220 ← ここで先手が必勝?
8手:33333333332 ←
のように各点の線の本数が決まる。図示すれば下図となる。
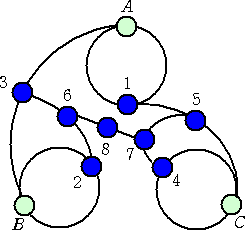
A、B、C、・・・、1、2、3、・・・ の順になるべく早く「引けなくする(値を3にする)」ように埋
めていく。
6手目で終了するには、線の本数が「2」の点が3つあるが、それらが2つ以上の閉路で区
切られ、別々の3つの領域に配置されていればよい。
同じ領域に「2」以下の点が2つ以上あれば、それらを結ぶことができる。
閉路を構成するのは、「3」の点列である。最少数は2個となる。
点が一列に並んでいるとすると、 {3,2,3, 3,2,3, 3,2,3} とすればよい。
具体的には、2つの閉路 A-1、3-C-5 で区切られた3つの領域 ※括弧数字が「2」の点
┌───┐┌───┐ ┌───┐
A─(2)─1 B─(4) 3─C─(6)─5
└───┘└─┘ └─────┘
手順: A-A、A-1、B-C、B-B、C-3、C-5 の順に線を引いていく。
3つの閉路 A-1、B-3、C-5 で区切られた4つの領域
┌───┐┌───┐┌───┐
A─(2)─1 B─(4)─3 C─(6)─5
└───┘└───┘└───┘
手順:A-A、A-1、B-B、B-3、 C-C、C-5 の順に線を引いていく。
がその一例である。
閉路を構成する条件は、3の個数をN(3)、2の個数をN(2)とすると、N(3)≧2N(2) の場合
は可能である。
7手目で終了するには、{…, 3,2,3, …, 3,2,3, …} ※…の部分には残りの「3」が入る
とすればよい。
N=1 の場合
A12
0手:000
1手:220
2手:332 ← 後手
N=2 の場合
AB12345
0手:0000000
1手:2020000
2手:2222000
3手:3322200
4手:3333220 ← ここで後手必勝?
5手:3333332 ←
N=4 の場合
ABCD123456789ab
0手:000000000000000
1手:200020000000000
2手:220022000000000
3手:330022200000000
4手:332022220000000
5手:332222222000000
6手:333322222200000
7手:333333222220000
8手:333333332222000 ←
9手:333333333322200 ← ここで先手が必勝?
10手:333333333333220 ←
11手:333333333333332 ←
N=5 の場合
ABCDE123456789abcde
0手:0000000000000000000
1手:2000020000000000000
2手:2200022000000000000
3手:3300022200000000000
4手:3320022220000000000
5手:3322022222000000000
6手:3333022222200000000
7手:3333222222220000000
8手:3333332222222000000
9手:3333333322222200000
10手:3333333333222220000 ←
11手:3333333333332222000 ← ここで先手が必勝?
12手:3333333333333322200 ←
13手:3333333333333333220 ←
14手:3333333333333333332 ←
FNさんからのコメントです。(平成2年11月24日付け)
問題の答えが「2N」とのことですが、正解だと思います。2N以上であることと、2N以下で
あることを示せばいいわけですが、2N以下であることは、実際に、2N手で終わるケースを
作ればいいわけで、攻略法さんの次の手順をそのまま一般化すればOKです。
3つの閉路 A-1、B-3、C-5 で区切られた4つの領域
┌───┐┌───┐┌───┐
A─(2)─1 B─(4)─3 C─(6)─5
└───┘└───┘└───┘
手順:A-A、A-1、B-B、B-3、 C-C、C-5 の順に線を引いていく。
あとは、2N以上であることの証明ですが...。攻略法さんの記号 N(3) と
N(2) の関係か
ら出そうです。終局した時点でN(3)≧2N(2)が成り立っていることとかを使えば...。

























