正方形をいくつかの部品に分解して正三角形を作る問題は多々ある。しかし、分割された
部品が互いに連結されたまま移動することによって正三角形（または正方形）ができること
に感動した。
これは、数学者の秋山 仁先生が以前ＴＶで実演されていた。このアイデアを用いた家具
も作られていた。
まず、下図のように正方形を分割する。（詳細は後述）
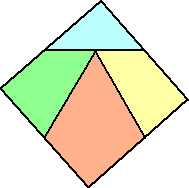
その分割された部品に対して、下図のように連結部分（青い点）を設ける。
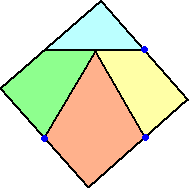
その連結部分を中心として、各部品を回転させる。
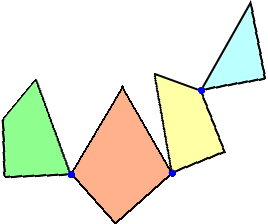
そうすると、下図のような正三角形が作られる。
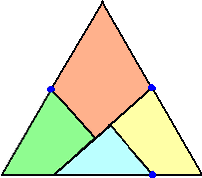
それでは、正方形をどのように分割したら、このような正三角形が作られるのだろうか？
闇雲に分割しても、それは失敗するばかりである。次のように考えればよい。
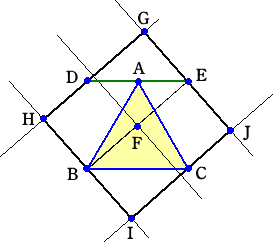正三角形ＡＢＣの頂点Ａを通り、長さがＢＣに等しく、ＢＣに平行な線分ＤＥをとる。
線分ＢＥの垂直２等分線と線分ＢＥの交点を
Ｆとする。
この垂直２等分線と線分ＥＦの長さを基にし
て正方形ＧＨＩＪの４頂点が定められる。
左図では、点Ａは線分ＤＥの中点として作図
したが、Ａの位置をずらすことによって、いろい
ろな造形の変化を楽しむことが出来るだろう。
上図から、「正方形と同じ面積を持つ正三角形が作れる」ことは明らかだろう。
特に、点Ａが線分ＤＥの中点とした場合を考える。
始めに与えられる正方形 ＧＨＩＪ の１辺の長さを ２ とすると、作図の解析から、
ＢＦ＝ＦＥ＝１
である。 このとき、正三角形 ＡＢＣ の１辺の長さを ａ とすると、
（ａ/２）2＋（
ａ/４）2＝１より、 ａ＝４
/７ となるので、この長さを１辺に持つ正三角形を作図すれば、上記のような手順で、面積４の正方形が作図され、さらに、正方形を上図のように切断すれば、正方
形と同じ面積を持つ正三角形を構成することが出来る。
それでは、逆に、最初に正三角形を与える場合はどうだろうか？
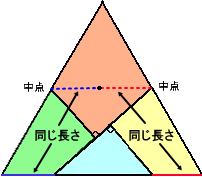
この場合も、上記と同様に、上図のように切り分ければ、面積の等しい正方形を作ること
ができる。
この話題が、
北大数学科（編） 中村 郁（監修）
北大高校生講座 数学の並木道 （日本評論社）
の、ｐ１０〜ｐ１２ に取り上げられている。
