今日、横浜での出張先で次の問題が話題になった。
log7 と比べて最も近い数は、log6 と log8 のうち、どれか?
対数表を持ち出して、
log6=0.7782 、log7=0.8451 、log8=0.9031
から、 log7−log6=0.0669 、 log8−log7=0.0580 なので、
log7 に最も近い数は、 log8 の方である
とするのでは、あまりにも味気なく芸がない。
上記の問題の眼目は、「直感的にどちらか?」を聞いているところだろう。
私自身、この問題を聞いて咄嗟に頭に浮かんだ方法は、グラフを活用するものである。
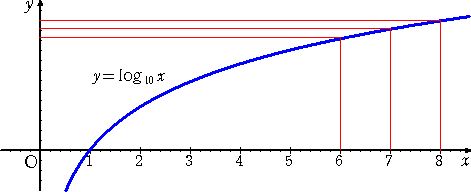
y=log10x は、上に凸の関数なので、x 軸の正の方向にいくにしたがって、勾配が緩や
かになる。そのことがグラフをイメージすることによって直ちに分かる。
だから、対数表を使うまでもなく、log8 の方が log7 に最も近いということが分かる。
ただ、グラフを用いる場合は、凸関数という解析的な性質を用いているので、高校生にと
っては少し荷が重いかもしれない。
次のように軽妙に計算する方が、この問題の解法としては適切かもしれない。
(解) (log7−log6)−(log8−log7)=2log7−(log6+log8)=log49−log48>0
よって、 log7−log6 > log8−log7 となり、log8 の方が log7 に最も近い。(終)
上記の計算から、次のことが一般的に成り立つことが分かる。
連続する3つの自然数 A 、B 、C (A<B<C) について、
logA よりも、logC の方が、logB の値に最も近い
(証) A=n−1 、B=n 、C=n+1 において、
B2−AC=n2−(n−1)(n+1)=1>0
なので、 常に、 logB−logA > logC−logB が成り立つ。 (終)
