BD、ACの交点をEとする。Ｅが次の条件を満たすとき、それぞれの四角形ABCDの面積Sを
求めよ。
(1) EはBDを3：4に内分する。
(2) EはBDを2：3に内分する。
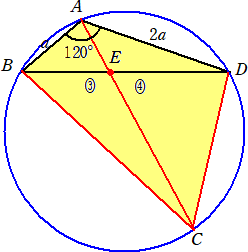
（コメント） とりあえず、（１）の図を描いてみた。
＝余弦定理より、 ＢＤ2＝ａ2＋４ａ2−４ａ2（−１/２）＝７ａ2 から、 ＢＤ＝
ａ正弦定理より、
ａ＝２ｓｉｎ１２０°＝
なので、 ａ＝（√２１）/７このとき、 ＡＢ＝（√２１）/７ 、ＤＡ＝２（√２１）/７ 、ＢＥ＝３
/７ 、ＥＤ＝４/７ で、△ＡＢＤ＝（１/２）・２ａ2・ｓｉｎ１２０°＝３
/１４ である。らすかるさんが考察されました。（令和７年１０月２１日付け）
多分うまい解き方があるのだろうと思いますが、全く思いつかなかったのでゴリゴリ計算し
ました。
BE ： ED=a ： b のとき、t=a/(a+b) とすると、AE ： EC=7t^2-4t+1 ： 7t(1-t)
これより、 (四角形ABCD)={(3t+1)/(7t^2-4t+1)}△ABD
ある角がθ、対辺が a、残る2辺の比が b ： c である三角形の面積は、
S=(a^2sinθ)/{2(b/c+c/b-2cosθ)}
であることから、 △ABD=3√3/14
よって、四角形ABCDの面積は、(3√3)(3t+1)/{14(7t^2-4t+1)} なので、
(1) t=3/7 を代入して、6√3/7
(2) t=2/5 を代入して、165√3/182
ＧＡＩ さんからのコメントです。（令和７年１０月２１日付け）
解答、ありがとうございます。２つとも同じ値になっていました。
自分のやり方に較べ、遥かに簡略な方法でらすかるさんは求められています。
（コメント） そうか、方べきの定理か．．．。らすかるさんの
BE ： ED=a ： b のとき、t=a/(a+b) とすると、AE ： EC=7t^2-4t+1 ： 7t(1-t)
を追認してみました。
ＡＢ＝（√２１）/７ 、ＤＡ＝２（√２１）/７ 、ＢＤ＝
である。ＢＥ ： ＥＤ＝a ： b のとき、 ＢＥ＝（ａ/（ａ＋ｂ））
そこで、 ａ/（ａ＋ｂ）＝ｔ とおくと、 ＢＥ＝ｔ
で、 ＥＤ＝（１−ｔ）∠ＡＢＤ＝θ とおくと、余弦定理から、
ｃｏｓθ＝（３/７＋３−１２/７）/（２・（√２１）/７・
）＝２/このとき、 ＡＥ2＝３/７＋３ｔ2−２・（√２１）/７・ｔ
・（２/）＝（３/７）（７ｔ2−４ｔ＋１）よって、 ＡＥ＝（（√２１）/７）√（７ｔ2−４ｔ＋１）
方べきの定理より、 ＡＥ・ＥＣ＝３ｔ（１−ｔ） なので、
ＥＣ＝３ｔ（１−ｔ）・（
/）/√（７ｔ2−４ｔ＋１）＝（√２１）ｔ（１−ｔ）/√（７ｔ2−４ｔ＋１）したがって、
ＡＥ ： ＥＣ＝（（√２１）/７）√（７ｔ2−４ｔ＋１）：（√２１）ｔ（１−ｔ）/√（７ｔ2−４ｔ＋１）
＝７ｔ2−４ｔ＋１ ： ７ｔ（１−ｔ）
＃ようやく、スッキリしました。らすかるさんに感謝します。
らすかるさんから追記をいただきました。（令和７年１０月２１日付け）
「簡略な方法」に見えるのは、おそらく「途中計算の大半を省略」したためかと思います。
公式っぽいものを出すだけで大変手間がかかっています。
△ABCにおいて、AB ： AC＝b ： c であるとし、∠A=θ、BC=a とする。
AB=bk、AC=ck とすると、余弦定理により、a^2=b^2k^2+c^2k^2-2bck^2cosθ
これを k について解くと、k=a/√(b^2+c^2-2bccosθ)
本問の場合は、a=√3、b=1、c=2、θ=120°なので、代入して k を求めると、
k=√3/√(1+4+2)=√(3/7)=√21/7 から、AB=bk=√21/7、AC=ck=2√21/7
また、各辺の2乗は、
a^2 、(bk)^2=a^2b^2/(b^2+c^2-2bccosθ) 、(ck)^2=a^2c^2/(b^2+c^2-2bccosθ)
簡略化のため、t^2=b^2+c^2-2bccosθ とすると、(bk)^2=a^2b^2/t^2 、(ck)^2=a^2c^2/t^2
これを、
# 各辺の長さの2乗をp,q,rとすると、三角形の面積はS=(1/4)√{2(pq+qr+rp)-(p^2+q^2+r^2)}
という変形ヘロンの公式に代入して整理すると、S=(1/4)√{2(pq+qr+rp)-(p^2+q^2+r^2)}
(途中計算省略)
=a^2/(4t^2)*√{(2b^2+2c^2-t^2)t^2-(b^2-c^2)^2}
=a^2/(4(b^2+c^2-2bccosθ))*√{(2b^2+2c^2-(b^2+c^2-2bccosθ))(b^2+c^2-2bccosθ)-(b^2-c^2)^2}
(途中計算省略)
=(a^2bcsinθ)/{2(b^2+c^2-2bccosθ)}
=(a^2sinθ)/{2(b/c+c/b-2cosθ)}
ここまでで、AB=√21/7、AC=2√21/7、S=(a^2sinθ)/{2(b/c+c/b-2cosθ)} が得られました。
次に、これを座標に当てはめます。
円を x^2+y^2=1 とし、B(-√3/2,1/2)、D(√3/2,1/2)
Bを中心として半径が√(3/7)である円：(x+√3/2)^2+(y-1/2)^2=3/7 と x^2+y^2=1 の交点
を求めると、A(-3√3/14,13/14)
Eは、t=0 のとき、Bに一致、t=1 のとき、Dに一致するように、
E=B+t(D-B)=((t-1/2)√3,1/2)
とします。
Aを通る直線の式を y=m(x+3√3/14)+13/14 とおくと、y軸に平行な直線を表せず問題があ
るので、 x=m(y-13/14)-3√3/14 とします。
これに、E((t-1/2)√3,1/2) を代入してmを求めると、m=-(7t-2)/√3
よって、直線の式は、
x=-{(7t-2)/√3}(y-13/14)-3√3/14=-(√3/42){9+(7t-2)(14y-13)}
これを、x^2+y^2=1 に代入してxを消去し、yの式を導出すると、
(1/588){9+(7t-2)(14y-13)}^2+y^2=1
(途中計算省略)
28(7t^2-4t+1)y^2-4(7t-2)(13t-5)y+13(13t^2-10t+1)=0
より、 y=13/14 、(13t^2-10t+1)/{2(7t^2-4t+1)}
AEのy座標の差は、13/14-1/2=3/7
ECのy座標の差は、1/2-(13t^2-10t+1)/{2(7t^2-4t+1)}=3t(1-t)/(7t^2-4t+1)
よって、AE：EC=3/7：3t(1-t)/(7t^2-4t+1)=(7t^2-4t+1)：7t(1-t) なので、
AE：AC=(7t^2-4t+1)：(7t^2-4t+1)+7t(1-t)=7t^2-4t+1：3t+1
となり、 (四角形ABCD)={(3t+1)/(7t^2-4t+1)}△ABC が言えました。
DD++ さんからのコメントです。（令和７年１０月２３日付け）
これ、そんなにややこしいですかね？
円に内接する四角形ABCDとその対角線の交点Eについて、
AB*AD/AE = BC*BA/BE = CD*CB/CE = DA*DC/DE
が成り立ちます。（証明は三角形の相似で一瞬）
BC*BA/BE = DA*DC/DE
の部分を使います。
事前に、正弦定理で、BD =
は出しておきます。(1) AB = x とすると、AD = 2x で、CB = 3y とすると、CD = 2y
△ABDと△CBDに注目して、余弦定理より、7x^2 = 7y^2 = 3
よって、求める面積は、S = (x^2 + 3y^2) *
/2 = 6/7(2) AB = x とすると、AD = 2x で、CB = 4y とすると、CD = 3y
△ABDと△CBDに注目して、余弦定理より、7x^2 = 13y^2 = 3
よって、求める面積は、S = (x^2 + 6y^2) *
/2 = 165/182らすかるさんからのコメントです。（令和７年１０月２４日付け）
やはり簡単な解き方があったのですね。全く思いつきませんでした。
（コメント） DD++ さんの解法は、素晴らしい切れ味ですね！感動しました。
（AB*AD/AE = BC*BA/BE の証明）
△ＥＡＤ∽△ＥＢＣ より、AD ： ＡＥ＝ＢＣ ： ＢＥ から明らか。
他も同様。
