このうち、1から4まで隣同士のとき、なぞっていくことができるのは、8通りある。
(例)
1→2
↓
4←3
3×3の場合 1〜9まで配置。同様に考えると、3つのパターンがあり、全部で、8×3通り
でしょうか?
(コメント) 全部で、 (4+8+8)×2=40(通り) かな?
実際に、2×2の場合、
の4パターンで、1の配置方法が、それぞれ2通りあることから、求める場合の数は、
4×2=8(通り)
3×3の場合、
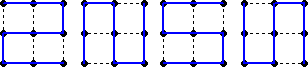
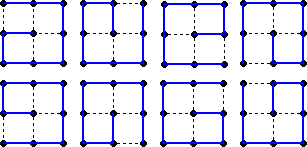
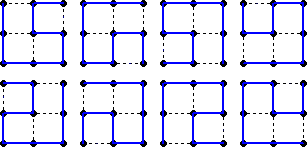
の20パターンで、1の配置方法が、それぞれ2通りあることから、求める場合の数は、
20×2=40(通り)
らすかるさんからのコメントです。(令和7年6月21日付け)
1が左上隅のパターンが8通り、1が中央のパターンが8通り なので、
8×4+8=40(通り) だと思います。
(参考:「A096969」)
以下、工事中!
