たときは、200くらいでしたが。確かに、有名なフェルマー点や、ナポレオン点などあります。
チェバの定理で、比を適当に変えればいくらでも作れそうです。中でも有名な、外心O、内心I、
重心G、垂心Hについて、考察しました。便宜上、鋭角三角形に限定します。(内部にあるため)
先ず、簡明な、△ABCについて、その辺の中点をD、E、Fとした場合、△ABCと△DEFの重
心は一致します。それで、△ABC(G)=△DEF(G)と表記します。
次に、△ABCの外心をとります。各辺の中点で作る三角形の垂心を考えるとOに一致しま
す。したがって、△ABC(O)=△DEF(H)
以前にも、似た内容を投稿しましたが、
「△ABC(□)=△DEF(☆) 但し、D、E、Fは、A、B、Cに由来」を考察します。
ks さんからのコメントです。(令和7年5月21日付け)
△ABCの垂心をHとする。各辺の垂心の足をD、E、Fとすると、Hは、△DEFの内心になる。
したがって、△ABC(H)=△DEF(I)
△ABCの内心を I とする。内接円の各辺との接点をD、E、Fとすると、I は、△DEFの外心
になる。したがって、△ABC(I)=△DEF(O)
これで、H→I→O→H となりましたが、逆の I→H→O→I の場合、見つけていただけないで
しょうか?
ks さんからのコメントです。(令和7年5月23日付け)
△ABCの外心をO、OA=a、OB=b、OC=c とするとき、
重心 OG=(a+b+c)/3
垂心 OH=a+b+c なので、OH=3OG (オイラー線)
ks さんからのコメントです。(令和7年5月24日付け)
△ABCの外心(O)、垂心(H)、内心(I)、重心(G)の4個のうち、いずれかの二つが、一致
するとき、△ABCが正三角形であるための必要十分条件になります。
ks さんからのコメントです。(令和7年5月26日付け)
△ABCの垂心をHとする。Hの各辺による対称点をD、E、Fとする。△DEFの内心がHに一
致するので、△ABC(H)=△DEF(I)
ks さんからのコメントです。(令和7年5月27日付け)
△ABCの内心を I とする。I のそれぞれの辺対称な点をD、E、Fとする。△DEFの外心は、
I に一致するので、△ABC(I)=△DEF(O)
ks さんからのコメントです。(令和7年5月28日付け)
△ABCの外心をOとする。各辺による、点Oの対称点をD、E、Fとすると、△DEFの垂心は、
Oに一致するので、△ABC(O)=△DEF(H)
H→I→O→H となりましたが、逆順の例はないでしょうか?
ks さんからのコメントです。(令和7年5月29日付け)
△ABCの垂心をHとする。Hから各辺への垂線の足の延長した線が、外接円と交わる点を
D、E、Fとすると、△DEFの内心は、Hに一致する。したがって、△ABC(H)=△DEF(I)
(コメント) 証明してみた。
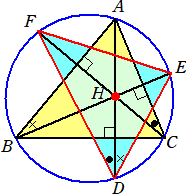
上図において、 ∠ADF=∠ACF 、∠ADE=∠ABE
さらに、 90°−∠ACF=90°−∠ABE より、 ∠ACF=∠ABE
よって、 ∠ADF=∠ADE となり、線分ADは∠EDFの2等分線である。
同様にして、線分BEは∠DEFの2等分線、線分CFは∠DFEの2等分線である。
以上から、Hは△DEFの内心となる。
ks さんからのコメントです。(令和7年5月30日付け)
逆に、△ABCの内心を I とするとき、頂点と内心を通る直線が外接円との交点をそれぞれ
D、E、Fとすると、△DEFの垂心は、I と一致するので、△ABC(I)=△DEF(H)
また、△ABCの外接円をOとするとき、円周上のどの三点D、E、Fをとっても
△ABC(O)=△DEF(O)
証明は、簡単ですが、…。
(コメント) △ABC(I)=△DEF(H)を証明してみた。
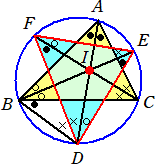
上図において、 2(●+○+×)=180° から、 ●+○+×=90°
よって、DI⊥EF 、EI⊥FD 、FI⊥DE となるので、I は、△DEFの垂心となる。
以下、工事中!
