以前というか、随分と前に、京大数学に出てた

　tan((ａ＋ｂ)/２)≦(tan(ａ)＋tan(ｂ))/２

という不等式を、敢えて凸不等式を使用せずに、図形的に見るやり方を考えてみました！

　他にも色々と解釈できると思うので、面白いやり方が有れば教えてください！

（証明）　ａ＝０　または　ｂ＝０　のときは明らか。

　０＜ａ＜π/４、０＜ｂ＜π/４　のとき、下図のように、円に内接する鋭角三角形ＡＢＣを考
える。

　　

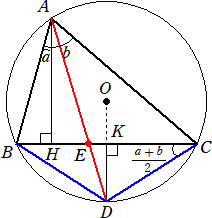
　ＢＣ＝２とすると、　ＡＨ・ｔａｎ（ａ）＋ＡＨ・ｔａｎ（ｂ）＝２　より、　ＡＨ＝２/（ｔａｎ(ａ)＋ｔａｎ(ｂ)）

　方べきの定理より、　ＡＨ・ＤＫ≦ＡＥ・ＤＥ＝ＢＥ・ＣＥ≦１　・・・　(*)

なぜなら、ＢＥ＝ｘ　とおくと、ＣＥ＝２−ｘ　より、　ＢＥ・ＣＥ＝ｘ（２−ｘ）＝−（ｘ−１）²＋１≦１

よって、(*)より、　２/（ｔａｎ(ａ)＋ｔａｎ(ｂ)）・ｔａｎ（（ａ＋ｂ）/２）≦１　なので、

　tan((ａ＋ｂ)/２)≦(tan(ａ)＋tan(ｂ))/２

が成り立つ。　　（証終）


（コメント）　鮮やかですね！



　　以下、工事中！