一般化と考えていいのでしょうか?
りらひいさんからのコメントです。(令和7年3月10日付け)
三線極点(trilinear pole)と三線極線(trilinear polar)のことですよね?(→ 三線極線)
これが何かの一般化なのかどうか私は知りませんが、円や二次曲線の極・極線とは無関
係だと思った方がいいと思います。よくあることですが、別のものに同じような名称が使われ
ていると紛らわしいですよね。
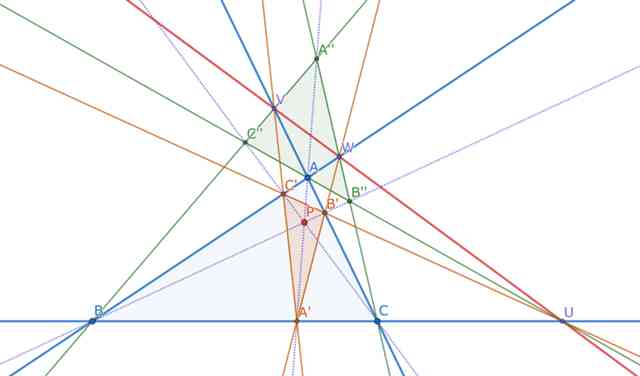
下の図で基準三角形を△ABCとするとき、点Pと直線UVWが三線極点・三線極線の関係
にあります。
りらひいさんからのコメントです。(令和7年3月11日付け)
上図について、説明を書いておこうと思います。
以下では射影平面で考えることとし、ユークリッド平面で必要な平行線の場合分けを一切
省略します。
点から始める場合と直線から始める場合でそれぞれ説明ができますが、それぞれの説明
は射影幾何の双対の関係にあります。
(1)[点Pから始める場合]
基準三角形を△ABCとします。点Pは直線BC、CA、AB上にない点とします。
BCとAPの交点をA',CAとBPの交点をB',ABとCPの交点をC'とするとき、△A'B'C'を(△ABC
に関する)点Pのチェバ三角形といいます。
基準三角形△ABCとチェバ三角形△A'B'C'は点Pを中心とする配景の位置にあるので、
デザルグの定理により配景の軸が存在します。
すなわち、BCとB'C'の交点U,CAとC'A'の交点V,ABとA'B'の交点Wはある直線l上にあり、
この直線lを(△ABCに関する)点Pの三線極線といいます。
また、A、A'に関する点Pの調和共役点をA'',B、B'に関する点Pの調和共役点をB'',C、C'
に関する点Pの調和共役点をC''とするとき、△A''B''C''を(△ABCに関する)点Pの反チェバ
三角形といいます。
4点A、U、B''、C''と4点B、V、C''、A''と4点C、W、A''、B''はそれぞれ一直線上にあります。
基準三角形△ABCと反チェバ三角形△A''B''C''は点Pを中心とする配景の位置にあるので
デザルグの定理により配景の軸が存在しますが、それは直線lに一致します。
(2)[直線lから始める場合]
基準三角形を△ABCとします。直線lは点A、B、Cを通らない直線とし、直線lと直線BC、CA、
ABの交点をそれぞれU、V、Wとします。
3直線AU、BV、CWを辺とする三角形を△A''B''C''とします。
(BVとCWの交点をA''、CWとAUの交点をB''、AUとBVの交点をC''とします。)
基準三角形△ABCと△A''B''C''は直線lを軸とする配景の位置にあるので、デザルグの定理
により配景の中心が存在します。
すなわち、3直線AA''、BB''、CC''はある点Pで交わり、この点Pを(△ABCに関する)直線lの
三線極点といいます。
また、BC、AUに関する直線lの調和共役線を i とし、CA、BVに関する直線lの調和共役線を
j とし、AB、CWに関する直線lの調和共役線を k とするとき、3直線 i、j、k を辺とする三角形
を△A'B'C'とします。
(jとkの交点をA'、kとiの交点をB'、iとjの交点をC'とします。)
4直線BC、AA''、j、k と4直線CA、BB''、k、i と4直線AB、CC''、i、j はそれぞれ一点で交わ
ります。
基準三角形△ABCと△A'B'C'は直線lを軸とする配景の位置にあるので、デザルグの定理
により配景の中心が存在しますが、それは点Pに一致します。
以下、工事中!
