本日気になってあちこち調べまくりましたが、どうやら未解決のようです。
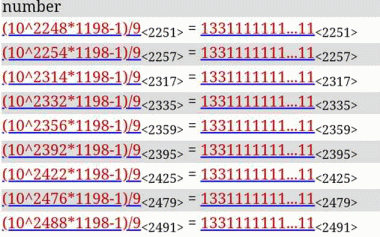
2000 以下の n については合成数と判明していて、2001 から 2500 までの範囲では、下記
の図に登場している n 以外で合成数と判明しています。下記図の n については、合成数か
素数かについてわかっていないようです。
らすかるさんからのコメントです。(令和7年3月6日付け)
「133」の後に1をn個つなげて素数になる最小のnは2890ですから、それらの値はすべて合
成数とわかっています。
実際、それらの値をPari/GPで、isprime((10^2248*1198-1)/9)のように調べると、すべて(1秒
以内で)0(つまり合成数)と判定されます。(→ 参考:「A069568」)
「A069568」のページのデータは、私が2023年に、a(119)〜a(602)を追加するまでは
a(1)〜a(118)までしかありませんでした。「603」の後に1を何個続けると素数になるかは、お
そらく誰もわかっていないと思います。(少なくとも30万個までは合成数でした。)
Dengan kesaktian Indukmu さんからのコメントです。(令和7年3月6日付け)
らすかるさん、偉業ですね。
※ (11980000*(1000000^(n))-1)/9 → 実はこちらの変種でもがいておりました。
a(603) が不明とのこと、大変に心惹かれます。
白状しますと、MAGMA で以下のコードで走らせて素数がみつかっていなかったので悲しいです。
for n in [4000] do
p := (1198 * 10^n - 1) div 9;
if IsPrime(p) then
printf "n = %o, candidate = %o\n", n, p;
end if;
end for;
Python で下記を走らせたところ、たしかに、n = 2890 で素数となりました。
from sympy import isprime
# n を 2889 から 2891 の範囲で調べる
n_range = range(2889, 2892)
# 結果を格納する変数
prime_results = []
for n in n_range:
P_n = (1198 * 10**n - 1) // 9 # 整数値を計算
if isprime(P_n):
prime_results.append((n, P_n)) # n とその素数を記録
prime_results # 結果を出力
らすかるさんからのコメントです。(令和7年3月6日付け)
※ (11980000*(1000000^(n))-1)/9 → 実はこちらの変種でもがいておりました。
(10^n*1198-1)/9 は、nが奇数のとき、11で割り切れ、
n≡0 (mod 6)のとき、7で割り切れ、n≡2 (mod 6)のとき、3で割り切れますので、
素数になるとしたら、n≡4 (mod 6) しかありません。それを表したのが、
(11980000*(1000000^(n))-1)/9
ですね。
(つまり、「変種」すなわち、この形にならない(10^n*1198-1)/9は合成数なので、調べる必要
がないということです)
らすかるさんからのコメントです。(令和7年3月7日付け)
n=2890の次に素数になるのは、n=17710 でした。ただし、n=17710 のときの値は確率的素
数です。
Dengan kesaktian Indukmu さんからのコメントです。(令和7年3月8日付け)
らすかるさん、有難うございます。C言語で組まれていますか?
らすかるさんからのコメントです。(令和7年3月8日付け)
はい、C言語です。
kuiperbelt さんからのコメントです。(令和7年3月8日付け)
レピュニット擬きについて、
2〜9の後に1が続く数で素数になるものを調べてみたら、素数になるのは、1が100個以下
の場合で、
2の後に1が2,3,12,18,23,57個
3の後に1が1,2,5,10,11,13,34,47,52,77,88個
4の後に1が1,3,13,25,72個
5の後に1が5,12,15,84個
6の後に1が1,5,7,25,31個
7の後に1が1,7,55個
8の後に1が2,3,26個
9の後に1が2,5,20,41,47,92個
となりました。7と8の場合が少ないので、7と8について1が1000個以下の場合まで調べてみると、
7については1が1,7,55個の他は素数は現れず、8については1が110,141,474,902個の場合も
素数になりました。
ただし、474個の場合と902個の場合は、Online MAGMA calculatorでは決定的素数判定
法であるECPP法で計算が終わらなかったので、確率的素数です。
さらに、7について1が6000個以下の場合まで調べましたが、1が1,7,55個の他は素数になり
ませんでした。
レピュニット数の数字を1つだけ別の数に置き換えた数で、素数となるものをニアレピュ
ニット素数(Near Repunit Prime)というそうです。
現在見つかっている最大のニアレピュニット素数(確率的素数)は2014年12月に発見された
(64*10^762811-1)/9=711111...111だそうです。
らすかるさんからのコメントです。(令和7年3月9日付け)
それらは数列サイト(https://oeis.org/Axxxxxx)の以下の項目にありますね。
21111…111が素数: A056700
31111…111が素数: A056704
41111…111が素数: A056706
51111…111が素数: A056713
61111…111が素数: A056717
71111…111が素数: A056719
81111…111が素数: A056722
91111…111が素数: A056726
また、関連するものは以下の通りです。
13333…333が素数: A056698
23333…333が素数: A056701
43333…333が素数: A056707
53333…333が素数: A056714
73333…333が素数: A056720
83333…333が素数: A056723
17777…777が素数: A089147
27777…777が素数: A056702
37777…777が素数: A056705
47777…777が素数: A056708
57777…777が素数: A056715
67777…777が素数: A056718
87777…777が素数: A056724
97777…777が素数: A056727
19999…999が素数: A002957
29999…999が素数: A056703
49999…999が素数: A056712
59999…999が素数: A056716
79999…999が素数: A056721
89999…999が素数: A056725
ちょうど今、これらの未開拓な部分について計算しているところです。17777…777は一つ見
つけましたので、先月追加しました。
あと、Pari/GPでは4500桁ぐらいまでは決定的素数判定法で素数かどうか調べられます。
ただし、4500桁となるとメモリが12GB、時間が(最近のPCで)15時間程度必要です。私のPC
はメモリが16GBしかありませんのでこの程度が限界ですが、さらにメモリがあれば5000桁ぐ
らいまではいけると思います(ただし数日〜1週間ぐらいかかります)。
そんな感じなので、8111…111の474個、902個はPari/GPでは1分程度で決定的素数と判
定できます。
H.Nakao さんからのコメントです。(令和7年3月11日付け)
数列「A069568」に対して、1≦n≦602については、
Toshitaka Suzuki, Table of n, a(n) for n = 1..602
https://oeis.org/A069568/b069568.txt
にて、計算済みなので、603≦n≦2000について、Pari/GPのisprime()関数を使って、計算し
てみました。結果は、次の通りです。(→ 素因数分解計算結果)
「???」は、a(n)が決定できなかったもの(-1または5001以上)です。
603≦n≦2000の範囲で、a(n)が決定できなかったnは、以下の21個です。
603,617,708,749,936,1023,1100,1133,1167,1222,1244,1353,1519,1530,1672,1750,1761,1793,
1861,1904,1937
以下、工事中!
