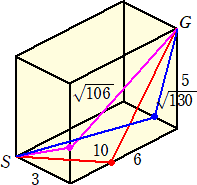
３辺の長さが 3、5、6 (底面3×6；高さ5)の直方体では、底面の一角Sにクモがいて天井の
向かいの一角Gにハエがいるものとする。

　クモはハエをめがけて直方体の表面を直進するとする。この時ちょうど10の距離で到着で
きるコースが発生する。

　コース取りを誤ると、√130 と最短でも整数でもない値になってしまう。また、同じ直方体
でも、底面 5×6;高さ3 でもSからGへのコースは最短10（誤れば、√106)が確保される。

　そこで、各辺の長さが整数で、最大辺が10まで取れるとするとき、向かい合う角へ直方体
の表面を最短距離が整数値で辿れる直方体が何通り存在しているかを問う。


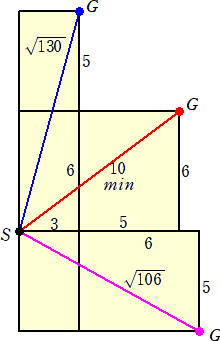
（コメント）　上記を絵にまとめてみました。

　らすかるさんからのコメントです。（令和７年１月１６日付け）

　私の解釈が正しければ、

(1,3,3), (2,2,3), (1,2,4), (2,6,6), (3,5,6), (4,4,6), (1,5,8),(2,4,8), (3,3,8), (7,8,8), (3,9,9), (4,8,9), (5,7,9),
(6,6,9)

の14通りだと思います。ちなみにこれで正しいならば、最大辺が

100までなら2060通り、1000までなら281334通り、10000までなら36553574通り、
100000までなら4487105091通り、1000000までなら532281148674通り、
10000000までなら61589103127262通り、100000000までなら6995157501115431通り、
1000000000までなら783139679297467648通り


　ＧＡＩ さんからのコメントです。（令和７年１月１６日付け）

　私も初めは、らすかるさんが出された数値でOKだと思ていたんですが、展開図を書いて
確認していた中で、(2,9,10)の組み合わせも可能なはずだよな？(底面２×9;高さ10とか)

　これが何故取ってこれないのかを考え直し、改めてプログラムをし直して、

(1,6,7),(2,5,10),(2,9,10),(3,5,9),(4,5,8),(5,5,7),(5,6,6),(5,8,10),(6,8,9)

の9個も考えられなくもないと思い直しました。

　あとは人工知能を搭載してない私は、展開図を書きながら最短距離が整数となるかを見て
行くと、(5,6,6)の組合せだけ最短距離が√157で整数となるコースどりでは13とはなれるも最
短ではないことになってしまう!

　他の8個は最短を確認できました。

　以上から、異なる直方体の種類は、14+8=22 でないかと思っているところです。

　私も初めに作っていたプログラムでは100まででは2060通りとなっていました。でも今は確か
めようもなくどうだろう？と思っているところです。


　らすかるさんからのコメントです。（令和７年１月１６日付け）

　(2,9,10)の場合

√((2+9)^2+10^2)=√221　、√((2+10)^2+9^2)=15　、√((9+10)^2+2^2)=√365　、√221＜15＜√365

となり、最短の√221は整数ではないので不適では？

　あと、もし「3方向のうち最短であるものが整数」でなく、「3方向のうちどれかが整数」でよい
ならば、(5,6,6)も√((6+6)^2+5^2)=13で整数なので、(5,6,6)も含めて23通りにしないとおかしい
と思います。
（つまり、22通りとなる考え方はあり得ないのでは、という意味です）


　ＧＡＩ さんからのコメントです。（令和７年１月１６日付け）

　そうか！直方体の向かい合う角に向かうルートは3通り出来るので、そのうちの最短が整
数とならなければいけないのが条件でしたから、追加しようとした9個は全くこの条件を満た
しませんね。

　ついつい自分が書いた展開図のみに従って判断していました。



　　以下、工事中！