ておりませんでした。
問題 単位円周上の任意のｎ個の点について、それらまでのｎ個の距離の積が２以上にな
るような点が、円周上、または、円の内部に存在することを示せ。
皆さまの、この問題に対するさまざまなアプローチを見てみたいです。さらに、本問に関連す
る数学的事実などご存知でしたら、教えてください。
ａｔ さんからのコメントです。（令和７年１月５日付け）
単位円周上のn点を、z_1、z_2、 … 、z_n とし、多項式 P(w)＝(w-z_1)*(w-z_2)*…*(w-z_n)
を考える。
|P(w)|≧２ かつ 1≧|w| なる w の存在が次のようにして示せる。
(z_1)*(z_2)*…*(z_n)＝(−１)^n となるように座標を設定できる。
k＝1、2、…、n に対して、w_k＝exp(i*2*π*k/n) とすると、
P(w_1)＋P(w_2)＋…＋P(w_n)＝2*n
であることがわかる。よって、|P(w_1)|＋|P(w_2)|＋…＋|P(w_n)|≧2*n
よって、|P(w_1)|、|P(w_2)|、…、|P(w_n)| のうち、少なくとも１つは２以上。
（コメント） ｎ＝１ のとき、単位円周上の点Ｐ1（１，０）に対して、Ｑ（−１，０）とおけば、
Ｐ1Ｑ≧２ である。
ｎ＝２ のとき、単位円周上の点Ｐ1（１，０）、Ｐ2（−１，０）に対して、Ｑ（０，１）とおけば、
Ｐ1Ｑ*Ｐ2Ｑ＝
×≧２ｎ＝３ のとき、単位円周上の点Ｐ1（１，０）、Ｐ2（−１/２，
/２）、Ｐ3（−１/２，−/２）に対して、Ｑ（−１，０）とおけば、
Ｐ1Ｑ*Ｐ2Ｑ*Ｐ3Ｑ＝２×１×１≧２
・・・・・・・・・・・・・・・・
確かに、条件を満たす点は存在しそう．．．。
Dengan kesaktian Indukmu さんからのコメントです。（令和７年１月６日付け）
特殊な場合では、こうなっているようです。
単位円に内接する正 ｎ＋１ 角形の頂点のうち n 個をとります。それらまでの ｎ 個の距離の
積が ２ 以上になる点が、円周上ないしは円の内部に存在することを示せ。
↓↓↓
正 ｎ＋１ 角形の頂点のうち ｎ 個をとったときにあぶれた頂点を P とします。
P から あらかじめとられていた ｎ 個の頂点に引いた線分の長さの積 N は ｎ＋１ に等しい。
不思議……。
（コメント） ｎ＝３、４の場合について、「不思議」さを体験してみました。
ｎ＝３ のとき、
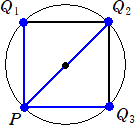
このとき、 Ｎ＝ＰＱ1・ＰＱ2・ＰＱ3＝
・２・＝４ｎ＝４ のとき、
このとき、 Ｎ＝ＰＱ1・ＰＱ2・ＰＱ3・ＰＱ4＝（２−２ｃｏｓ７２°）（２−２ｃｏｓ１４４°）
ここで、 ｃｏｓ１４４°＝−ｃｏｓ３６°＝−（
＋１）/４ 、ｃｏｓ７２°＝（−１）/４ なので、Ｎ＝ＰＱ1・ＰＱ2・ＰＱ3・ＰＱ4＝（５−
）/２・（５＋）/２＝５DD++ さんからのコメントです。（令和７年１月９日付け）
「または、円の内部」がわざわざついているのが気になっているんですが、この積が最大
値をとる点は、必ず円周上にあるわけでもないんですかね？
感覚的には、必ず円周上と言えそうな気がしていますが、さりとて証明もできず。
Dengan kesaktian Indukmu さんからのコメントです。（令和７年１月２１日付け）
双対多角形を利用すべきと直感的に思ったのですが、今日まで鼠一匹捕れませんでした。
(円の内部にもあるとしたら……)
kuiperbelt さんからのコメントです。（令和７年１月２２日付け）
1の原始(n+1)乗根をzとすると、z^(n+1)=1で、z^i(i=0,1,2,...,n)は複素数平面上で正(n+1)角形
となります。
zの複素共役z^*は、z^*=z^-1 なので、実軸上の点(x,0)とz^i(i=1,2,...,n)との距離の積の2乗は、
(x-z)*(x-z^-1)*(x-z^2)*(x-z^-2)*...*(x-z^n)*(x-z^-n)
=(x-z)*(x-z^n)*(x-z^2)*(x-z^(n-1))*...*(x-z^n)*(x-z)
=((x-z)*(x-z^2)*...(x-z^n))^2
となります。
(x-1)*(x-z)*(x-z^2)*..(x-z^n)=x^(n+1)-1=(x-1)*(x^n+...x^2+x+1) なので、
(x-z)*(x-z^2)*...(x-z^n)=x^n+...x^2+x+1
と表すことができて、実軸上の点(x,0)とz^i(i=1,2,...,n)との距離の積は、|x^n+...x^2+x+1| となり
ます。
x=1 のときは、x^n+...x^2+x+1=n+1 となって、距離の積はn+1となります。
x=0 のときは、(0,0)とz^i(i=1,2,...,n)との距離は1なので、それらの積も明らかに1ですが、
((-z)*(-z^2)*...*(z^n))^2=(-z)^(n(n+1)/2*2)=(-z)^(n(n+1))=(-1)^(n(n+1))*z^(n(n+1))=1*1=1
となるので、距離の積は1となります。
実軸上の点(x,0)とz^i(i=1,2,...,n)との距離の積|x^n+...x^2+x+1|は、xについて連続な実数値関
数なので、中間値の定理から、距離の積が2となる点は(0,0)と(1,0)の間にあることになります。
--------------------------------------------------------------
1の原始(2k+1)乗根をzとすると、z^(2k+1)=1で、z^i(i=0,1,...,2k)は複素数平面上で正(2k+1)角
形となります。
実軸上の点(x,0)とz^i(i=0,1,...,2k)との距離の積の2乗は、
(x-1)^2*(x-z)*(x-z^-1)*(x-z^2)*(x-z^-2)*...*(x-z^2k)*(x-z^-2k)
=((x-1)*(x-z)*(x-z^2)*...(x-z^2k))^2=(x^(2k+1)-1)^2
となります。
x=-1 のとき、(x^(2k+1)-1)^2=(-2)^2=4 となるので、(-1,0)とz^i(i=0,1,...,2k)との距離の積は
2となります。
--------------------------------------------------------------
1の原始2k乗根をz、原始4k乗根をwとすると、n=2k,w^2=z,w^4k=z^2k=1で、w^i(i=0,1,...,4k-1)
は複素数平面上で正4k角形となり、w^(2i+1)(i=0,1,...,2k-1)は複素数平面上で正2k角形となり
ます。
実軸上の点(x,0)とw^(2i+1)(i=0,1,...,2k-1)との距離の積の2乗は、
(x-w)*(x-w^-1)*(x-w^3)*(x-w^-3)*...*(x-w^(4k-1))*(x-w^-(4k-1))
=(x-w)*(x-w^(4k-1))*(x-w^3)*(x-w^(4k-3))*...*(x-w^(4k-1))*(x-w)
=((x-w)*(x-w^3)*...*(x-w^(4k-1)))^2
となります。
(x-w)*(x-w^3)*(x^w^5)*...*(x-w^(4k-1))=(x-w)*(x-w*z)*(x-w*z^2)*...*(x-w*z^(2k-1))
=x^2k-w^2k=x^2k+1
なので（x^2k-1=0の根と係数の関係を応用）、x=±1のとき、x^2k+1=2 となるので、(±1,0)と
w^(2i+1)(i=0,1,...,2k-1)との距離の積は2となります。
Dengan kesaktian Indukmu さんからのコメントです。（令和７年１月２３日付け）
DD++ さんからのコメント；
「または、円の内部」がわざわざついているのが気になっているんですが、この積が最大
値をとる点は、必ず円周上にあるわけでもないんですかね？
の問いかけについて、ぼんやりと想起したのが以下です。
複素関数論における最大値の原理（または最大値の定理）
《正則関数f(z)を、円の中心からある一定の距離までの範囲で定義されていて、この範囲で
値がなめらかに変化する関数とします。このとき、f(z)の大きさを表す|f(z)|の最大値は、その
範囲の端っこの部分、つまり円周上で必ず見つかります。》
このような f がみつかると嬉しいなと。
※でも、大数の記事中の問題に、複素関数論を使うのかと．．．。近道があるのですかね。
Dengan kesaktian Indukmu さんからのコメントです。（令和７年１月２４日付け）
冒頭の問題について、以下のような予想を立てました。
ｎ≧３ の場合について、以下を予想します。
単位円上の任意のｎ点について、単位円上に点Pが存在し、その点からの距離の積Mにつ
いて不等式 M＞(4/π)^n が成り立つ。
(自信がありません)
Tabasco さんからのコメントです。（令和７年２月６日付け）
私が作った解法も、複素平面によるものでした。なぜ「円の内部」とわざわざ記述されてい
るかについての考察、興味深く拝見いたしました。
Dengan kesaktian Indukmu さんからのコメントです。（令和７年３月７日付け）
ツイッターで紹介されていたサイトに、以下のページがありました。
(下の画像はその一部をトリミングしたものです)
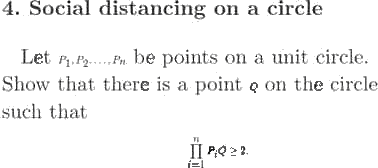
文面が「on the circle」であり、「in the circle」ではないことから、求める点は円周上にある
と意識されていることと存じます。
以下、工事中！
