直角三角形ＡＢＣにおいて、Ｃ＝９０°とし、ＢＣ＝ａ、ＣＡ＝ｂ、ＡＢ＝ｃ とおく。
∠ＡＢＣ＝３θ とし、辺ＣＡ上に、∠ＤＢＣ＝θ となる点Ｄをとる。
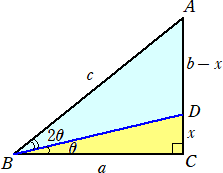
このとき、 ａ・ｔａｎθ＋２ｃ・ｓｉｎθ＝ｂ が成り立つ。
（証明） △ＡＢＤにおいて、正弦定理より、
（ｂ−ｘ）/ｓｉｎ２θ＝ｃ/ｓｉｎ（π/２＋θ）＝ｃ/ｃｏｓθ
ｓｉｎ２θ＝２ｓｉｎθｃｏｓθ なので、 （ｂ−ｘ）/（２ｓｉｎθ）＝ｃ すなわち、 ｂ−ｘ＝２ｃ・ｓｉｎθ
ここで、 ｘ＝ａ・ｔａｎθ なので、 ａ・ｔａｎθ＋２ｃ・ｓｉｎθ＝ｂ が成り立つ。 （証終）
この等式を用いると、次の等式が簡単に示される。
（１） ｔａｎ（π/９）＋４ｓｉｎ（π/９）＝
（２） ｔａｎ（π/１２）＋２
ｓｉｎ（π/１２）＝１（３）
ｔａｎ（π/１８）＋４ｓｉｎ（π/１８）＝１（証明）（１） θ＝π/９ のとき、 ３θ＝π/３ なので、 ａ ： ｂ ： ｃ＝１ ：
： ２よって、 ｔａｎ（π/９）＋４ｓｉｎ（π/９）＝
が成り立つ。（２） θ＝π/１２ のとき、 ３θ＝π/４ なので、 ａ ： ｂ ： ｃ＝１ ： １：
よって、 ｔａｎ（π/１２）＋２
ｓｉｎ（π/１２）＝１ が成り立つ。（３） θ＝π/１８ のとき、 ３θ＝π/６ なので、 ａ ： ｂ ： ｃ＝
： １： ２よって、
ｔａｎ（π/１８）＋４ｓｉｎ（π/１８）＝１ が成り立つ。 （証終）上記では、等式 「ｔａｎ３θ＝ｂ/ａ のとき、ａ・ｔａｎθ＋２ｃ・ｓｉｎθ＝ｂ」 を利用して、
「ｔａｎ（π/９）＋４ｓｉｎ（π/９）＝
」などを示したが、もちろん直接示すことも可能である。（証明） π/９＝θ とおくと、 ３θ＝π/３ なので、 ２θ＝π/３−θ である。
このとき、 ｓｉｎ２θ＝ｓｉｎ（π/３−θ）＝（
/２）ｃｏｓθ−（１/２）ｓｉｎθすなわち、 ２ｓｉｎθｃｏｓθ＝（
/２）ｃｏｓθ−（１/２）ｓｉｎθ両辺を ｃｏｓθ で割って２倍すれば、 ４ｓｉｎθ＝
−ｔａｎθ となる。したがって、 ｔａｎ（π/９）＋４ｓｉｎ（π/９）＝
が成り立つ。 （証終）他の（２）（３）については、読者の方の練習問題としよう。
同様にして、「ｔａｎ４θ＝ｂ/ａ」のときに成り立つ等式を調べてみよう。
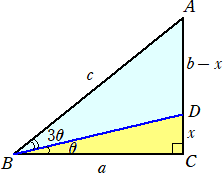
このとき、 ａ・ｓｉｎθ＋ｃ・ｓｉｎ３θ＝ｂ・ｃｏｓθ が成り立つ。
（証明） △ＡＢＤにおいて、正弦定理より、
（ｂ−ｘ）/ｓｉｎ３θ＝ｃ/ｓｉｎ（π/２＋θ）＝ｃ/ｃｏｓθ
よって、 ｂ−ｘ＝ｃ・ｓｉｎ３θ/ｃｏｓθ
ここで、 ｘ＝ａ・ｔａｎθ なので、 ａ・ｔａｎθ＋ｃ・ｓｉｎ３θ/ｃｏｓθ＝ｂ が成り立つ。
したがって、 ａ・ｓｉｎθ＋ｃ・ｓｉｎ３θ＝ｂ・ｃｏｓθ （証終）
この等式を用いると、次の等式が簡単に示される。
（１）
ｓｉｎ（π/２４）＋２ｓｉｎ（π/８）＝ｃｏｓ（π/２４）（２） ｓｉｎ（π/１６）＋
ｓｉｎ（３π/１６）＝ｃｏｓ（π/１６）（３） ｓｉｎ（π/１２）＋２ｓｉｎ（π/４）＝
ｃｏｓ（π/１２）証明は、前のものと同様である。
よおすけさんからのコメントです。（令和６年６月２５日付け）
一般化したら、おそらくこれだろうという等式を挙げました。
直角三角形ＡＢＣで、∠ＡＢＣ＝ｎθ、∠ＤＢＣ＝θ のとき、
ａ・ｓｉｎθ＋ｃ・ｓｉｎ(ｎ−1)θ＝ｂ・ｃｏｓθ
※ｎは２以上の整数
以下、工事中！
