・　意外な所に正三角形　 　　　　　　　　　　　　Ｓ．Ｈ氏

　下図のように、正三角形ＡＢＣの各辺上に点Ｐ、Ｘ、Ｑ、Ｙ、Ｒ、Ｚをとり、六角形ＰＸＱＹＲＺ
を作る。ただし、六角形ＰＸＱＹＲＺの各辺の長さは等しいものとする。

　　　　　　　　　　

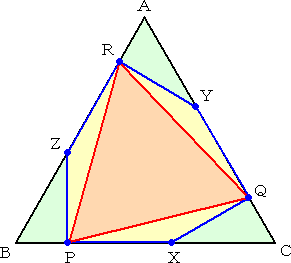
　このとき、△ＰＱＲは正三角形になるという。

（証明）　ベクトルＰＸを、ＰＸで表すことにする。

　　　　六角形ＰＸＱＹＲＺは閉じているので、　ＰＸ＋ＸＱ＋ＱＹ＋ＹＲ＋ＲＺ＋ＺＰ＝０

　　ところで、ＰＸ、ＱＹ、ＲＺはつりあっているので、　ＰＸ＋ＱＹ＋ＲＺ＝０

　　　よって、　ＸＱ＋ＹＲ＋ＺＰ＝０　が成り立つ。

　　このとき、　ＸＱ・ＹＲ＝ＹＲ・ＺＰ＝ＺＰ・ＸＱ＝−(１/２)｜ＸＱ｜²　となる。

　　したがって、ＸＱとＹＲ、ＹＲとＺＰ、ＺＰとＸＱのなす角は、すべて１２０°である。

　　△ＡＢＣは正三角形なので、∠ＣＸＱ＝∠ＡＹＲ＝∠ＢＺＰ　が成り立つ。

　　　よって、　∠ＰＸＱ＝∠ＱＹＲ＝∠ＲＺＰ　から、　△ＰＸＱ≡△ＱＹＲ≡△ＲＺＰ

　　したがって、　ＰＱ＝ＱＲ＝ＲＰ　となり、△ＰＱＲは正三角形になる。（証終）


　条件を満たす六角形は無数に作れるが、意外と「六角形の各辺の長さは等しい」という
条件が思いのほか強くて、与えられた正三角形ＡＢＣと美しい調和をなすことに感動した。