y−y1={(y2−y1)/(x2−x1)}(x−x1)
で使う公式があるが、
x(y1−y2)−y(x1−x2)+x1y2−x2y1=0
と変形されるので、行列式を利用して
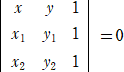
と表される。この形式にしておけば、
3点 A(x1,y1)、B(x2,y2) 、C(x3,y3) を通る円の方程式は、
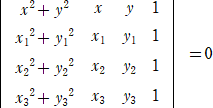
また、空間でも、
3点 A(x1,y1,z1)、B(x2,y2,z2)、C(x3,y3,z3) を通る平面の方程式は、
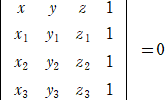
同じく、
4点 A(x1,y1,z1)、B(x2,y2,z2)、C(x3,y3,z3) 、D(x4,y4,z4) を通る球面の方程式は、
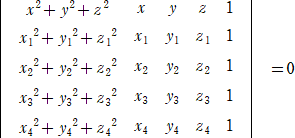
*勿論、半径を正の実数でとれるように4点を選ぶ必要はあります。
などで構成できるようです。
(幾つかで実験しただけで証明したわけではありませんが・・・)
りらひいさんからのコメントです。(令和6年3月28日付け)
5点 A(x1,y1)、B(x2,y2) 、C(x3,y3)、D(x4,y4)、E(x5,y5) を通る広義の二次曲線(*)
の方程式は、
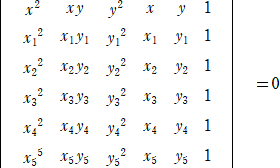
*広義の二次曲線…「非退化二次曲線(楕円・放物線・双曲線)」、「2直線」、「1点」、「1直線」
垂心系をなさない4点 A(x1,y1)、B(x2,y2) 、C(x3,y3)、D(x4,y4) を通る広義の直角双
曲線(**)の方程式は、
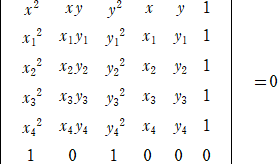
あるいは、式変形すれば、
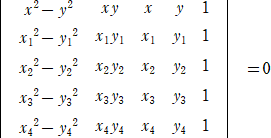
**広義の直角双曲線…「狭義の直角双曲線(漸近線が直交する双曲線)」、「直交する2直
線」、「1直線」
因みに、5点A、B、C、D が垂心系をなす場合、上式の左辺は、(x,y) に依らず恒等的に
0になります。
これが意味するのは、任意の点が(4点を通る)広義の直角双曲線上にあるということです。
実際のところは、垂心系をなす4点を通る広義の直角双曲線が無数に存在し、この4点を
除く任意の点はそれらのうちの1本の上にあります。
GAIさんが載せた円の方程式も、次のように書けば、2次曲線に条件付加されたものとい
うのがわかりやすくなります。
ただ、この式は行列式の展開と基本変形により簡単にGAIさんの式になるので、メリットは
あまりありませんが……。
3点 A(x1,y1)、B(x2,y2) 、C(x3,y3) を通る広義の円(***)の方程式は、
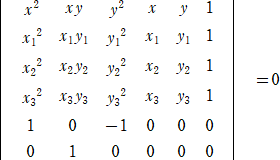
***広義の円…「狭義の円」、「1直線」
以下、工事中!
