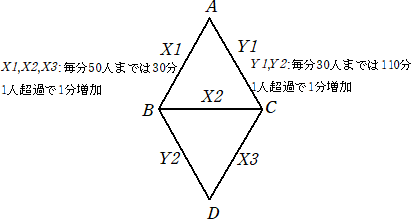
A-B 間、B-C 間、C-D 間には、それぞれ移動手段 X1、X2、X3 があります。各 X は、利
用者が毎分 50 人以下であれば人数に関わらず 30 分で到着し、利用者が毎分 50 人を超
える場合は 1 人超えるごとに所要時間が 1 分増加します。
A-C 間、B-D 間には、それぞれ移動手段 Y1、Y2 があります。各 Y は、利用者が毎分
30 人以下であれば人数に関わらず 110 分で到着し、利用者が毎分 30 人を超える場合は
1 人超えるごとに所要時間が 1 分増加します。
これについて、以下の 2 つを考えてください。
(1) ある日、A 市から D 市まで、毎分 70 人が移動しようとしました。各々自分の所要時間
が最短になるよう経路を選択する場合、移動に合計何分かかるでしょうか?
(2) 実際にはその日の早朝に B-C 間の X2 にトラブルが発生し、終日利用不可になってし
まいました。しかしそれでも、A 市から D 市まで、毎分 70 人が移動しようとしました。各々
自分の所要時間が最短になるよう経路を選択する場合、移動に合計何分かかるでしょうか?
GAI さんからのコメントです。(令和6年2月13日付け)
(1) 8300(分)
________(20人)________
|<------------------->|
A--(50人)--B--(30人)--C--(50人)--D
|_______(20人)________|
(2)10150(分)
_______(35人)________
|<------------------>|
A--(35人)--B--(0人)--C--(35人)--D
|_______(35人)_______|
DD++ さんからのコメントです。(令和6年2月14日付け)
総計じゃなくて、各個人の所要時間でお願いします。
(2) は 10150/70 = 145 分で正解です。
(1) は……これどういう計算になったんでしょうか?
あ、わかりました、合計っていうのが誤解を招いたんですね。
例えば、(2) の場合、
Y1→X3 のルートを通った人は、Y1 で 110+5 分、X3 で 30 分、合計 145 分
X1→Y2 のルートを通った人は、X1 で 30 分、Y2 で 110+5 分、合計 145 分
いずれの場合も所要時間の合計は 145 分。
と、合計というのはこういう意味のつもりでした。
GAI さんからのコメントです。(令和6年2月14日付け)
はい。合計って、何をもっての合計だろうとずっと思っていたんですが、各々自分の所要
時間の表現があったので、全員の所要時間の合計で比較してしまいました。
後はプログラムで70人の分岐の仕方を分類し、(1)では全部で2556通りに分類でき、かか
る全員のタイムの合計での集計での最小値探しを、(2)では上記のB-C間の通行が0人のパ
ターン(全部で71通り)を集め、この中での最小値を探しました。
所要時間は何人が同じルートを選択しているかによって異なってくるので、一個人だけで
最短時間のコースは選べないから、どうしても統計的処理になってしまいました。
(1)は、(50+30+50)(人)*30(分)+(20+20)(人)*110(分)=8300(分)です。
また第2位は、
A-B:50|B-C:31|C-D:51|A-C:20|B-D:19(人) で、(50+31)*30+51*31+(20+19)*110=8301(分)
または、A-B:51|B-C:31|C-D:50|A-C:19|B-D:20(人) で、
51*31+(31+50)*30+(19+20)*110=8301(分) の移動で起こる。
ちなみに、(1)の正解は何ですか?140(分)ということなんでしょうか?
DD++ さんからのコメントです。(令和6年2月14日付け)
(1) はその人数にはなりませんね。というのは、Y1→X3 の経路を通ろうとする人は、
110+30 = 140 分かかることになりますが、X1→X2→X3 に変更すれば、
(30+1)+30+30 = 91 分で済み、こちらに使用経路を変更するはずだからです。
プログラムで考えるなら、こう考えてみてください。
手順 1:70 人それぞれに番号をつけ、ランダムな経路を選択する
手順 2:1 番の人から順に、「もし自分が他の経路に変更したら自分の所要時間が短くなる
場合、そっちに変更する」を 70 番の人まで実行
手順 3:手順 2 で誰か 1 人でも変更があった場合、誰も変更しなくなるまでさらに手順 2 を
繰り返す
手順 4 :各々の移動時間が何分になったかを出力
もし可能であれば、X2 が完全に運休するのではなく、
・遅延で +5 分かかる場合
・遅延で +10 分かかる場合
・遅延で +15 分かかる場合
……
・遅延で + 70 分かかる場合
も出してみてください。面白いことになります。
GAI さんからのコメントです。(令和6年2月16日付け)
DD++ さんの説明を十分理解していないかも知れませんが、誘導に従って考えてみると、
1人目は当然各駅を通るコースで、 30+30+30=90(分) で行く。
2人目も、 30+30+30=90
以下、50人目も、90
51人目は、条件より、 31+31+31=93
52人目は、 32+32+32=96
・・・・・・・
66人目は、 46+46+46=138
ここで、67人目はこのコースだと、 47+47+47=141 だが、
A-Cコース+C-Dコースを選択すれば、 110+30=140 なので、こちらが短時間となり、コ
ースを変更して進むことになる。
この変更を行っても、それ以前の人はなんらコースを変更する必要は感じない。
以下、68、69、70人目も当然このコースでいくことを選択する。
(各自の所要時間は同じく140分)
だから、70人が移動するのに140分が最小時間と考えてしまうのですが、どこの何がおかし
いのでしょう?
なお、70人の所要時間は皆同じでなくてもバラバラでも構わないのでしょうか?
DD++ さんからのコメントです。(令和6年2月16日付け)
GAI さんが誤解されているポイントは 2 つです。
1 つめ:「51人目は、条件より、 31+31+31=93」ですが、渋滞による遅延は自分が何人目か
ではなく、一気に何人通ろうとしているかで決まります。
(通る人数を「70 人」ではなく「毎分 70 人」としているのはこのため)
つまり、51 人が X1-X2-X3 を選択するのは、51 人目が 93 分かかるのではなく、51 人全
員が 93 分かかることを意味します。
2 つめ:「67人目はこのコースだと、 47+47+47=141 だが、A-Cコース+C-Dコースを選択
すれば、 110+30=140」
ですが、X3 は渋滞が発生しているので 後者は 110+47 = 157 分になりますね。
(これも、移動が「毎分 70 人」であることに注意してください)
なお、70人の所要時間は皆同じでなくてもバラバラでも構わないのでしょうか?
構いませんが、しかしその場合は遅いルートから早いルートに変更したがる人がどこかに
いると思います。だから、毎分人数が非整数でもよいとすれば、結果的には全員同じ所要
時間に収束するはずです。
整数人数限定で考える場合は、1 分の差は残るかもしれませんね。
GAI さんからのコメントです。(令和6年2月17日付け)
考えれば考えるだけ混乱してくるんですが、66人の集団で各市を巡れば(Xの手段のみ)か
かる時間は各自共通で46*3=138分ですよね。
もし、Yの移動手段を使えば、AからD市に一人でも最低110+30=140分の時間での非効率
の行き方なので、70人が一斉に移動する手段はYの手段を取り入れないのがよく、単純に
Xだけの移動手段で70人が共通に50*3=150分を使えば、これが最短の所要時間になるん
ではないのかな?
DD++ さんからのコメントです。(令和6年2月17日付け)
そうです。(1) は 150 分で正解です。全員が X を利用した場合でも 50 分なので、どんな
場合でも Y を 1 回利用するより X を 2 回する方が短く済みます。
よって、全員が X のみを利用することになり、所要時間は 50*3 = 150 分です。
一方で、改めて (2) の場合、145 分が正解です。
X2 が運休しているので経路が完全に分離した 2 つしかなく、渋滞がなければどちらの経
路も同じ時間です。
ということは全員渋滞の影響が少ない方へ行こうとするので、各経路を 35 人ずつが利用
して、所要時間は 115+30 = 145 分です。
・・・ということで。
A-D 間の交通のみを考えるなら、X2 は存在する方が交通の便が悪くなる奇妙な経路なの
でした。
これがゲーム世界の話で本当に A-D 間の移動しか行われないなら、X2 は即刻撤廃すべ
きということになります。
現実では B 市や C 市の住人もいるでしょうから X2 撤廃とは行かないでしょうけど。
DD++ さんからのコメントです。(令和6年2月19日付け)
参考として。
X2 に渋滞とは別原因で遅延が発生し、所要時間が 30 分からふえた場合を 5 分刻みで
計算したものがこちらです。
(毎分の人数なので、経路利用者数は非整数もアリとしています)
BC 間 合計時間(毎分の X1-X2-X3 経路利用者数)
30 分 …… 150 分(50 人)
35 分 …… 155 分(50 人)
40 分 …… 160 分(50 人)
45 分 …… 158 分 20 秒(145/3 人)
50 分 …… 156 分 40 秒(140/3 人)
55 分 …… 155 分(45 人)
60 分 …… 153 分 20 秒(130/3 人)
65 分 …… 151 分 40 秒(125/3 人)
70 分 …… 150 分(40 人)
75 分 …… 145 分(35 人)
80 分 …… 140 分(0〜30 人)
85 分 …… 145 分(0 人)
90 分 …… 145 分(0 人)
95 分 …… 145 分(0 人)
以下ずっと145分(0 人)
あまりに直感的でない結果なんですが、なんでこんな現象が起こるんでしょうね?
以下、工事中!
