セッションが行われ、参加してきた。
（発表会場の、７号館３階を望む）
率直な感想で、レベルの高さに圧倒された。流石に日本を代表する高校生たちだ。数学
はもちろん、ゲームやルービックキューブの話まで考察の範囲は広く、指導される先生方の
苦労がひしひしと伝わってくる。
一番驚かされたのは、初見で発表を聞いていた中学３年の生徒が、発表とは異なる解答
をしばらく考えて示していたこと。実に明解な別解だった。
問題 １/ｓｉｎ１０°＝
ｔａｎ７０°＋１ を示せ。発表者の生徒によれば、この問題は、高１の試験で出題されたもので、当時誰も解けな
かったことから、興味を持って取り組んだという。
中３の生徒は、次のように鮮やかに解かれた。筑駒生、恐るべしである。
頂角２０°の２等辺三角形ＡＢＣを考え、ＢＣ＝２とする。内部に正三角形ＢＣＤをとる。
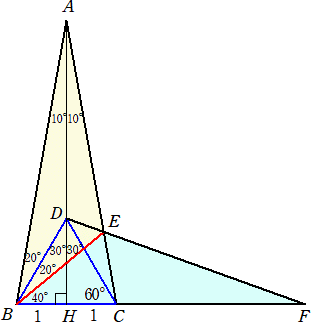
辺ＡＣ上に、∠ＤＢＥ＝２０°となる点Ｅをとり、直線ＤＥと直線ＢＣの交点をＦとおく。
このとき、∠ＢＥＣ＝６０°なので、４点Ｂ、Ｃ、Ｅ、Ｄは同一円周上にあるので、
∠ＣＤＥ＝４０°となり、 ∠ＣＦＥ＝２０° が分かる。
よって、両端の角とその間の辺相等で、 △ＡＢＥ≡△ＦＢＥ から、 ＡＢ＝ＢＦ
ところで、△ＡＢＨにおいて、 ＡＢ・ｓｉｎ１０°＝１ から、ＡＢ＝１/ｓｉｎ１０°
また、ＤＨ＝
で、∠ＨＤＦ＝７０°から、 ＢＦ＝ｔａｎ７０°＋１よって、 １/ｓｉｎ１０°＝
ｔａｎ７０°＋１ が成り立つ。（コメント） 生徒同士が純粋に数学について、活発に議論している姿に感動しました！
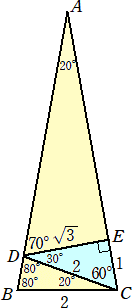
DD++ さんから別解をいただきました。（令和６年１月１６日付け）
上記の等式、私も以前考えたことがあって、もっとシンプルな証明を見つけていますので
投稿します。
頂角 A = 20°の二等辺三角形 ABC を考え、BC = 2 とします。辺 AB 上に ∠BCD = 20°
となるように点 D をとり、辺 AC 上に CE = 1 となるように点 E をとります。
