道に巻き付けたとすると、どれだけの隙間を一周全体で空けることが出来るか?
#しめ縄は、「注連縄」と書かれる。
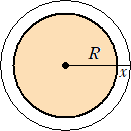
の問いに対して、赤道半径をRとして、2*π*R+1=2*π*(R+x) から、x=1/(2*π)=0.159154・・・
で、約16(cm) と驚かされた。(Rの値には依存しない!)
そこで、同じ設定で、巻き付けたひもを一方に可能な限り引っ張りよせ、巻き付けた部分
以外はピンとひもを張って、なるだけ空高い部分でひもを結ぶ様子を想像して欲しい。
さて、この様にして、1(m)伸ばしたひもを赤道上でこの様に再び貼りて付けて行ったとする
と、ひもはどれだけ高い位置に上げることが可能か?
但し、地球は完全楕円体とし、赤道半径は、6378137(m)とする。(Wikipediaより)
DD++ さんからのコメントです。(令和5年12月29日付け)
巻きつきが地面から離れる 2 点をそれぞれ地球中心と結んだとき、その間にできる角度を 2θ とおきます。
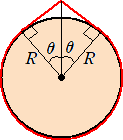
条件より、2Rtanθ + R(2π-2θ) = 2πR + 1 つまり、2tanθ - 2θ = 1/R
θ が微小だと思えば、tanθ は、tanθ ≒ θ + (1/3)θ^3 と近似できるので、
(2/3)θ^3 = 1/R
ここで、 cosθ ≒ 1- (1/2)θ^2 と近似できるので、
1/cosθ-1 ≒ (1/2)θ^2
よって、求める高さは、
R(1/cosθ-1) ≒ (1/2)Rθ^2 = (3/4)*(2R/3)^(1/3)
実際の値とは異なりますが、計算しやすい R≒6144000 だと 120 m なので、それよりもう
ちょっと高いくらいですかね。感覚的に 1km くらい行くかと思ってたのに意外と低い……。
計算ミスってないですよね?
GAI さんからのコメントです。(令和5年12月29日付け)
2tanθ - 2θ = 1/R 辺りをコンピュータ等の利用で、θを探すと、
θ=0,00617253・・・(rad) 辺りで、これから、最大 121.56060・・・(m) 程度になりました。
私の印象では、「こんなにも高くなるんかい!」の方での驚きでした。DD++ さんは逆なんで
すね。
直線と曲線はやっぱり違う性質を持っているんだな~(当たり前と言えば当たり前か?)
なお、この角度で、R*θ=39369(m) なので、最高になる地点から約40km東西でひもは地
面から離れ始めることになる構造です。
DD++ さんからのコメントです。(令和5年12月31日付け)
全体を浮かせる場合は、球が大きいと不利そう(実際はそうでもない)なのに対し、一箇所
だけ引っ張って浮かせるなら、球は大きければ大きいだけ有利なのが明らかですからねえ。
以下、工事中!
