自治医科大学の入試問題に次のようなものがある。
円に外接する正三角形の面積は、その円に内接する正三角形の面積の何倍か?
これは、平成教育委員会の問題になりそうなくらい、一般の人々が解いてみようと思うよ
うな問題である。絵が描ければ解決したも同然だろう。
正三角形において、内心と外心は一致するので、下図を得る。
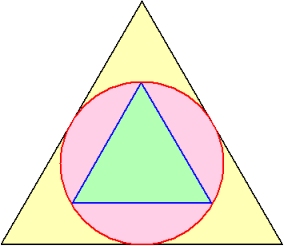
この絵のままでは難しいが、次のように内部の三角形を回転させると答えは明らかだろう。
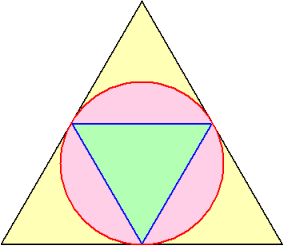
答えは、4倍となる。
クイズの問題だとこれで終わりだが、本題は、難関といわれる大学の入試問題である。果
たしてどのような意図を持って出題されたのか、また、途中の部分点等どのような配慮がな
されたのか、大いに気になる問題でもある。
そこで思うのは、出題者は上記のようなアクロバット的解法を期待していないのではないか
ということだ。
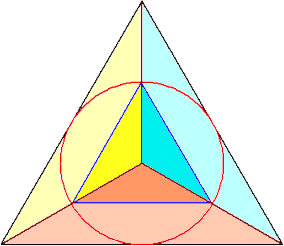
内心と三角形の各頂点を結ぶと2つの正三角形はそれぞれ3つの三角形に分割される。
それらの相似比は明らかに2:1である。したがって、面積比は、4:1 となる。
以上から、答えは、4倍となる。
以前は、このような解法を中学生で扱うことは十分可能であったが、今は出来ない。相似
比と面積比の関係が数学 I へ、内接円や外接円、重心が数学Aに移行してしまったからだ。
コツコツと地道な解法が数学では最も大事にされなければいけないと思うのだが、新学
習指導要領は、アクロバット的解法が出来ればよいという立場なのだろうか?この問題を
眺めていると、新学習指導要領の意図が不鮮明になってくるのを感じる。
