最近、相似比の計算で新しい技を覚えた。
長さが9の線分を折り曲げて2辺AB、BCとし、下図のような△ABCを作る。
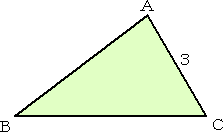
同様に、長さが9の線分を折り曲げて2辺PQ、PRとし、下図のような△PQRを作る。
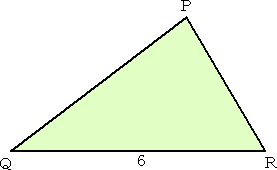
△ABCと△PQRが相似であるとき、相似比はいくつになるかという問題に対して、計算
に自信がある人は次のように解くであろう。
BC=X 、PR=Y とおくと、 X : 3 = 6 : Y 、 (9−X) : 3 = (9−Y) : Y
これより、XY=18 なので、(9−X)Y=3(9−Y) に代入して、 Y=15/4 を得る。
よって、相似比は、 AC : PR = 3 : 15/4 = 4 : 5
これに対して次のような解もあることを知って、とても感動した。
△ABCの周の長さは、12 で、△PQRの周の長さは、15
よって、相似比は、 12 : 15 = 4 : 5 (鮮やか!!)
相似比というと、辺の比という呪縛にとらわれて、辺の和の比という発想はなかなか浮か
ばないかもしれない。
