私の好きな定理に、デザルグの定理があります。この定理は定規だけで図を描くことがで
きます。また、パップスの六角形定理やその双対定理も定規だけで図が描けます。

　同じように定規だけで図が描ける定理に出会ったので紹介したいと思います。

　(射影)平面上に三角形ABCがある。

　直線BC上に異なる２点D₁、D₂を、直線CA上に異なる２点E₁、E₂を、直線AB上に異なる
２点F₁、F₂をとる。ただし、３点D₁、E₁、F₁は一直線上になく、３点D₂、E₂、F₂も一直線上
にないようにする。

　直線E₁F₁とE₂F₂の交点をP、直線F₁D₁とF₂D₂の交点をQ、直線D₁E₁とD₂E₂の交点を
Rとおく。

　このとき、次の２つの命題が成り立つ。

（１）　３直線AD₁、BE₁、CF₁が共点 ⇔ ３直線PD₂、QE₂、RF₂が共点

　　　

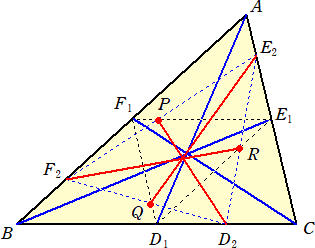
（２）　３直線AD₂、BE₂、CF₂が共点 ⇔ ３直線PD₁、QE₁、RF₁が共点

　（図は、（１）で、D₁、D₂の入れかえ、E₁、E₂の入れかえ、F₁、F₂の入れかえたもの）

＃この定理の双対定理も、定規だけで図が描けます。



　　以下、工事中！