2行2列の単位行列をE とします。X、Y、Z を、成分が複素数であるところの2行2列の行
列とします。a、b、c を実数(スカラー)とします。
任意の a、b、c について、
(a^2 +b^2 +c^2)*E = (a*X +b*Y +c*Z)^2
が成り立つように、X、Y、Z を【ひとくみ】定めてください。
#これを考えたのは、とある高名な物理学者です。天才。a^2 +b^2 +c^2 を因数分解して
しまっています。
ks さんからのコメントです。(令和4年12月7日付け)
ω^3=1 を成分にもつ行列かな?
GAI さんからのコメントです。(令和4年12月7日付け)
私も真似させてもらって、4行4列の単位行列をEとします。V、W、X、Y、Zを、成分が複素
数であるところの4行4列の行列とします。a、b、c、d、e を実数(スカラー)とします。
任意の a、b、c、d、 e について、
(a^2 )*E = (a*V )^2
(a^2 +b^2 )*E = (a*V +b*W )^2
(a^2 +b^2 +c^2 )*E = (a*V +b*W +c*X )^2
(a^2 +b^2 +c^2 + d^2)*E = (a*V +b*W +c*X + d*Y)^2
(a^2 +b^2 +c^2 + d^2 + e^2)*E = (a*V +b*W +c*X + d*Y + e*Z)^2
(a^2 +b^2 +c^2 + d^2 + e^2)^k*E = (a*V +b*W +c*X + d*Y + e*Z)^(2*k) (k=2,3,4,・・・・・)
が成り立つように、V、W、X、Y、Zを一組見つけて下さい。
Dengan kesaktian Indukmu さんからのコメントです。(令和4年12月7日付け)
掲示板における行列の表記法がよくわかりませんでしたので、OEISの真似をします。
2行2列の単位正方行列Eを、[1,0; 0,1] と書きます。行ごとの delimiter として ; で表すつ
もりです。
X = [0, 1 ;1, 0] 、Y = [0,-i ;i, 0] 、Z = [1, 0 ;0,-1]
としておくと、任意の実数 a、b、c について、 (a^2 +b^2 +c^2)*E = (a*X +b*Y +c*Z)^2
となります。
パウリ行列として知られているようです。
(コメント) なるほど!綺麗な結果ですね。
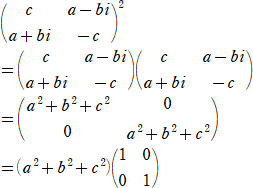
GAI さんからのコメントです。(令和4年12月8日付け)
四元数の i、j、k を用いると、 a^2+b^2+c^2= - (a*i + b*j + c*k)^2 としていいのかな?
Dengan kesaktian Indukmu さんからのコメントです。(令和4年12月8日付け)
GAIさんによる次のお題につきまして。
(a^2 +b^2 +c^2 +d^2)*E = (a*V +b*W +c*X +d*Y)^2
V = [0,0,0,1; 0,0,1,0; 0,1,0,0; 1,0,0,0]
W = [0,0,0,-i; 0,0,i,0; 0,-i,0,0; i,0,0,0]
X = [0,0,1,0; 0,0,0,-1; 1,0,0,0; 0,-1,0,0]
Y = [1,0,0,0; 0,1,0,0; 0,0,-1,0; 0,0,0,-1]
とするとよいようですね。
上は、物理学者ディラックが示したものを、GAIさんの表現にあわせたものです。ディラック
は上述のパウリ行列を拡張しました。
GAI さんからのコメントです。(令和4年12月9日付け)
Z=[0,0,i,0;0,0,0,i;-i,0,0,0;0,-i,0,0]
で行けると思います。パウリとディラックは、こんな型で繋がっているんですね。
以下、工事中!
