どんな向きで置いても、描かれている曲線との共有点を持つようにする。
このとき、曲線の長さの和の最小値は？
# 解の候補はありますが、それが正解かどうかはわかっていません。もちろん「曲線」には
「線分」も含みます。
（コメント） 題意を満たす場合として、下図のような配置を考えました。
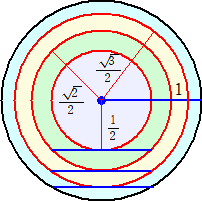
曲線の長さは、 ２π（１/２＋
/２＋
/２）＝π（１＋＋） となりますが、これが最小値という自信は全くありません。
DD++ さんからのコメントです。（令和４年９月１日付け）
最小値っぽい数値は確かにすぐに出ますが、本当に最小値かと言われると証明は難しい
ですね。まず、その値を取る曲線の書き方が無数に存在しますし……。
らすかるさんからのコメントです。（令和４年９月１日付け）
もしも、その「最小値っぽい数値」が 6 でしたら、それは最小値ではありません。6 ならば、
無数に存在しますけどね。
DD++ さんからのコメントです。（令和４年９月２日付け）
なんと。ハニカム構造が最強だろうと思ったらもっと効率いい引き方があるんですか。それ
は意外。
（コメント） π（１＋
＋）は明らかに論外でしたね！曲線の長さが６になる場合としては、下図があるのかな？
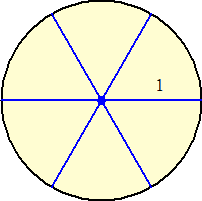
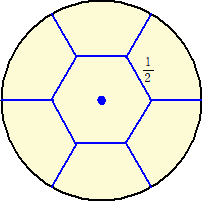
らすかるさんからのコメントです。（令和４年９月２日付け）
私もしばらく、6 の壁を越えられなかったのですが、2〜3日考えてようやく思いつくことがで
きました。因みに、その値は、約5.885 です。
案を思いついても、正確な長さの計算はかなり面倒でした。約5.885 という値は三重根号
を含んでいます。
DD++ さんからのコメントです。（令和４年９月４日付け）
２
＋６
−６≒５．９４９ という解はできたのですが、ここもらすかるさんが通った道でしょうか。だとすれば、もうちょっと短くなる可能性があって、かつ三乗根がでてきてもおか
しくない図形のアイデアが浮かぶのですが、ちょっとこれを計算する気力を絞り出すのは大
変……。
らすかるさんからのコメントです。（令和４年９月４日付け）
私は、その解は通過していないですね。なので、どんな図形なのかわからないので知りた
いです。
私は、6 からいきなり 5.885 に行きました。とはいっても、6より小さくする案を思いついて
から最小にするためにはどうこう・・・と、よく考えて図形を決めてから計算しましたが。
「計算する気力を絞り出すのは大変」の案が 5.885 かも知れませんね。
DD++ さんからのコメントです。（令和４年９月４日付け）
O(0,0)、A((
-+1)/2,0)、B(/2,(
-)/2)、C(/2,-(-)/2) として、OA、AB、AC をそれぞれ線分で結びます。
そうしてできた Y 字型を、O を中心に 90 度ずつ回して複製した図形です。
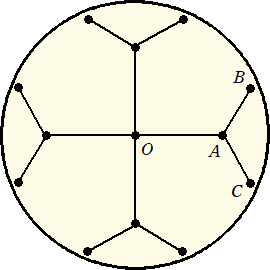
外側の隙間で長さ 1 が確保できないように 45 度ずつ 8 点取る発想で作りましたが、7 点
だと cos(2π/7) とか登場して 3 乗根になるよなー、と。
らすかるさんからのコメントです。（令和４年９月５日付け）
なるほど、面白い方法ですね。私の案とは方針が違いました。では、そろそろ私が思いつ
いた案を書きます。
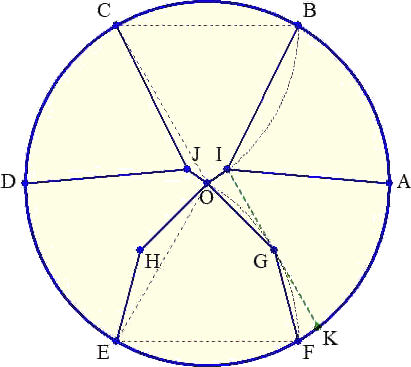
O(0,0)、A(1,0) として円周上を6等分するように、B、C、D、E、F をとります。
B(1/2,
/2)、C(-1/2,/2)、D(-1,0)、E(-1/2,-/2)、F(1/2,-/2) です。Eを中心とする半径1の劣弧FOに接し、直線OFと平行な直線と、Cを中心とする半径1の
劣弧OBの交点を I とします。
また、劣弧FOと直線の接点をGとします。FG=GO となります。座標は、
G((
-1)/2,-(-1)/2) 、I((√(4-3)+2-5)/4,(2+-√(12-9))/4)となります。y軸に関して、I と対称な点をJ、Gと対称な点をHとします。座標は、
H(-(
-1)/2,-(-1)/2) 、J(-(√(4-3)+2-5)/4,(2+-√(12-9))/4)です。そして、OI、IA、IB、OJ、JC、JD、OH、HE、OG、GFの各線分を描きます。
すると、長さの合計は、
√(30-16
+2√(120-207))+√(22-4-6√(4-3))+2(-)≒5.885となります。
半直線IG（劣弧FOの接線）と単位円の交点をKとすると、四角形OFKIは平行四辺形なの
で、IK=1 となります。
この線分 IK を、Gを通りながら、I 側の端を線分IOに沿ってO方向に、K側の端を弧FAに
沿ってA方向に移動すると、I 側の端がOに到達した時に長さが1となりますが、その移動途
中では1よりわずかに短くなります。
DD++ さんからのコメントです。（令和４年９月５日付け）
三重根号を三乗根と読み間違えていた……。
なるほど、上側で六方向への放射線を一部共有すれば、下方向に皺寄せが来てもお釣り
が出る、ということですね。私の案での中心部分の 90 度クロスに同じアイデア使ったらもっと
短くなるかな？
以下、工事中！
