(「対辺が平行」などの自明な特徴は除く)
DD++ さんからのコメントです。(令和4年5月12日付け)
外接円が存在する八角形で、各辺の長さ及び円の半径が全て自然数になっているもの。
……のうち最小のもの?(自信なし)
りらひいさんからのコメントです。(令和4年5月12日付け)
文章を読んだ瞬間に、「きっと対角線の長さがすべて整数なんだろうな」と思って確認した
ら、その通りでした。見事ですね。
らすかるさんからのコメントです。(令和4年5月13日付け)
私の予定回答は、りらひいさんの通りですが、DD++ さんが書かれたことも気になって調べ
ました。
その結果、「外接円が存在する八角形で、各辺の長さ及び円の半径が全て自然数になっ
ているもの。……のうち最小のもの」は、
「外接円の半径 8、辺の長さ 9、9、8、8、8、2、2、2 の八角形(辺は順不同)」
でした。
# これは半径が最小のもののうち、最長辺が最小であるものです。半径8の解は3つあり、
半径が最小のもののうち、面積が最小ならば別の解になると思います。
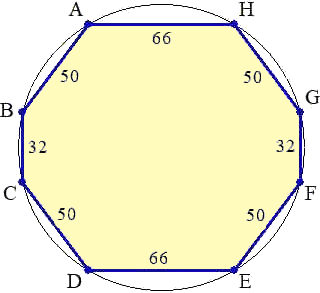
ただし、「外接円が存在する八角形で、各辺の長さ及び円の半径が自然数で、対辺がそ
れぞれ平行であるもののうち最小のもの」であれば、最初に書いた半径65の八角形になり
ます。
DD++ さんからのコメントです。(令和4年5月13日付け)
なるほど、「平行八角形」なら正解でしたか……。
ところで、辺の長さが 33、25、16 ではなく、全て2倍してあるのはどういう意図だったので
しょう?私はそこに違和感を覚えて、奇数の長さになっている線分、即ち、半径が整数となっ
ていることが何か重要なんだろうなと思っていたのですが……単にそういう八角形を探す方
法上での都合でしたか?
らすかるさんからのコメントです。(令和4年5月13日付け)
単なる探す時の都合です。
x^2+y^2=65^2上の点として、
(63,16)、(33,56)、(-33,56)、(-63,16)、(-63,-16)、(-33,-56)、(33,-56)、(63,-16)
の8点をとり、それぞれの点間の距離を計算していたので、結果的に偶数になりました。
半径を除けば、対角線の長さも含めてすべて偶数だったので、1/2にすることもできるな、
と後で思いましたが、1/2にしてしまうと座標で書くときとか外接円の方程式とかで、少し不
便になりますので、そのままにしました。
「どの3点も一直線上にないn点があり、どの2点間の距離も整数」のnに上限があるか?
というのを考えている途中経過なのですが、こういう八角形があることを考えると、上限はな
さそうな気がしています。
(ただし、点が増えると爆発的に長さの値が大きくなる気はしますが…)
DD++ さんからのコメントです。(令和4年5月13日付け)
なるほど、そういう研究の過程でしたか。
半径に制限をつけなければ、そのような点を同一円周上に無限に取れると思います。
任意の隣り合う頂点の間の中心角が「その半角の sin も cos も有理数になるような角度」
になるように点をとっておけば、どの頂点間の中心角も「その半角の sin も cos も有理数に
なる角度」なわけですから、単位円周上で任意の2点間の距離が有理数になるような点を好
きなだけ取れます。
ぐるっと回って戻ってきた最後の1個の中心角も条件を満たすのか、という点に関しても、
全ての中心角の合計が 2π であることから問題なし。
らすかるさんからのコメントです。(令和4年5月13日付け)
理論的な裏付けをありがとうございます。とりあえず、半径243061325の円に内接する192
角形で、すべての辺と対角線が整数になる具体値(192個の座標)までは出しました。
裏が取れたことで、これ以上進めても無意味なので、終了することにします。
GAI さんからのコメントです。(令和4年5月13日付け)
八角形にこだわらなければ、半径をいろいろ変化させると、それに内接するものがいろい
ろ作れていくのが面白いですね。(対角線の長さは無視です。)
例えば、半径を8としたら、8が等しい2辺に対し、残る1辺の長さが 4、11、14 の二等辺
三角形をそれぞれ 1、1、2個で埋めると、8の円に内接する四角形が納まる。
また、残る1辺の長さが 4、8、14の二等辺三角形なら、2、3、1個で内接する六角形が
納まる。(8を6個使えばこれも内接しているが・・・)
半径を9とすると、これに内接する六角形を
残る一辺の長さ (2,9,12) -> (1,3,2)個
(3,9,17) -> (2,3,1)個
(6,9,14) -> (2,3,1)個
当然 (9) -> 6個
以下、同様に、
