下図のように、縦３３、横３２の長方形を、異なる大きさの９個の正方形で埋め尽くす。

　ここで、例えば、�Hは、１辺の長さが９の正方形という意味。他も同様。

　　　　

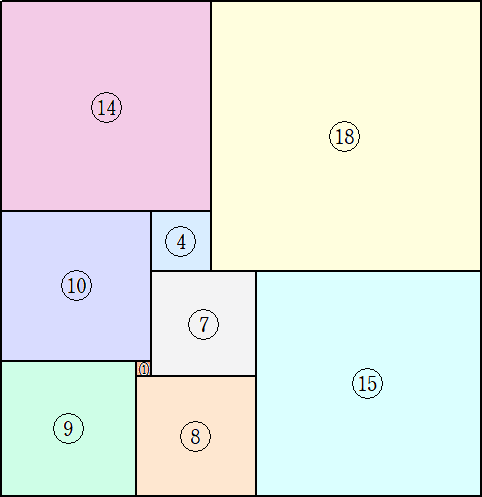
　この最後に埋めることになる１５を除いた他の８個のピースを、小さい順に並べると、

　　　１、４、７、８、９、１０、１４、１８

になっている。これを何気にOEISで検索してみたら、「A004710」にヒットして、

　　Positions of ones in binary expansion of Euler's constant gamma.

とある。　Euler's constant gamma　つまり、

　　γ:=lim(n->∞)(�納k=1,n]1/k-log(n))=0.57721･･･

である。この数値を二進法表示すれば、

　　γ=0.100100111100010001 1001111110001･･･(二)

　何と「1」の数字が発生する位置が小数点以下

　　1,4,7,8,9,10,14,18, (19,22,23,24,25,26,27,31,･･･)

と一致できているではないか！

　正にこれは偶然の一致でしかないが、でもここまで一致しているのは偶然にしては何か神
秘的に見えてしまうのは私だけの印象だろうか？



　　以下、工事中！