 平安朝の中頃、天禄元年(970年)に、7歳の息子のため
平安朝の中頃、天禄元年(970年)に、7歳の息子のために源為憲は「口遊」(くちずさみ)を作成した。
この文献は、「九九の表」が初めて現れたものとして有名で
ある。
左図の問題は、「竹束編」として残されているものである。
口遊 竹束編
今有竹束、周員二十一、問総数幾。
(同じ大きさの竹を束ねたら周りの本数が21本であった。このとき、竹の総数は何本か?)
上記の絵だけだと不明確だろう。詳しくは下図のように束ねられている。

この問いに対して、答えは次のようになっている。
周りの本数 21 に 3 を足して、それを二乗して、576 を得る。(←(21+3)2=576)
この 576 を 12 で割って、48 を得る。したがって、竹の本数は、48本である。
上記の計算で正しい答えが得られるわけであるが、そのからくりに興味を持った。
実際に実験してみると、
最初の出発点が竹 1 本の場合、 6 、12 、・・・ と、6 ずつ周りの竹は増えていく。
最初の出発点が竹 3 本の場合、 9 、15 、・・・ と、6 ずつ周りの竹は増えていく。
したがって、周りの本数が21本であったので、最初の出発点は竹 3 本の場合で、
求める値は、 3+9+15+21=48 となるわけである。
この計算をガウスの手法を用いて書き直すと、平安朝に知られていた解法が導かれる。
周りの本数を、L(=21)とする。 L を 6 で割った余りは、3 なので、次の和を求めれば
よい。
S=3+9+・・・+L
これは、初項が 3 で、末項が L、項数が (L+3)/6 の等差数列の和であるので、
S={(L+3)/6}×(3+L)/2=(L+3)2/12
となる。(→ (21+3)2/12=48)
上記の問題を現代の人が解けば、多分等差数列の和の公式を用いて解くと思うのだが、
平安朝の時代に、それと同様な結果となる術が知られていたわけで、これにはとても驚い
た!
(参考文献:藤原幸三郎、小林茂太郎 著 数学パズルの世界 (講談社))
(追記) 平成19年1月8日付け
上記の口遊 竹束編について、HPサイト「MM3210のホームページ 暗号 山上憶良」
の「間違っていた訂正」に興味ある記載がある。
『 竹の総数は、当然整数になるはずなのに、【術】には〈口伝〉として、
割りきれないとき、余りが割る数の半分以上ならぱ、1 とする。
となっているという。
なぜ割り切れない場合の処理のしかたが述べられているのだろうか?』
これに関して、MM3210さんは、「2次方程式の解法の存在を暗示しているのではない
か?」と述べられている。
MM3210さんから、この点について、詳しい説明を下記のように頂いた。
(平成19年1月9日付け)
『算学啓蒙』「堆積還源門第二問」 外周 L=6n の場合
【問】 ここに矢竹が一束ある。外周は54本である。全体はいくらか。
【答】 271本。
【術】 54本に6本加え、それに54をかけると、3240本になる。これを12で割って、芯
の1本を加える。
建部賢弘(1664-1739) は、この問題を三角数を使って解いています。すなわち、矢竹の
総数Sを、n番目の三角数 N=n(n+1)/2 が6個と、芯1の合計として、
S=6N+1=6n(n+1)/2+1=L(L+6)/12+1……(1)
と求めています。
『口遊』「竹束篇」 外周 L=6n−3 の場合
【問】 ここに竹の束がある。周囲の竹の数は21本である。総数は何本か。
【答】 48本。
【術】 周囲の竹の本数に3を加えて、2乗すると576になる。これを12で割ると48にな
る。
〈口伝〉によると、割りきれないとき、余りが割る数の半分以上ならぱ1とする。
ここでは12で割るから、6が割る数の半分である。
賢弘(1664-1739) の解法を参考にすれば、源為憲(?-1011)は、この問題を平方数を用い
て解いたのではないかと考えられます。
すなわち、竹の総数Sは、n番めの平方数 N=n2 と同積の菱形を3個合わせたものにな
るので、
S=3N=3n2 =3{(L+3)/6}2=(L+3)2/12……(2)
としたようです。
無論、為憲が、ガウス(1777−1855)の手法を用いたとは考えられません。
ところで、(2)に外周 L=6n を代入すると、
S=(L+3)2/12=(6n+3)2/12=3(n+1/2)2……(3)
正解は、(1)より S=3n(n+1)+1=3(n+1/2)^2+1/4……(4)
このように、(1)を用いて計算する外周 L=6n の問題を、外周 L=6n−3 用の(2)
で計算すると、1/4不足する数値が得られるので、〈口伝〉が意味を持つことになるわけで
す。
私は、この事実に基づいて、「2次方程式の解法の存在を暗示しているのではないか?」
と考えたわけです。なお、源為憲が、参議藤原為光の7歳の息子のために書いた『口遊』
には、「「いろは」47文字を用いて作成した、「たゐに」が載っています。参考までにいえば、
HPの「大伴家持と三平方の定理 」では、この「たゐに」を7段・7行に書けば三平方の定
理が証明できることを紹介しています。
(コメント) 以前、高校の教科書に、「三角数」や「四角数」という言葉が登場したことがあ
ります。(直ぐに消えてしまいましたが...)
MM3210さんのご説明、古文書等を拝見させていただくと、かなり和算の方
で培われた考え方なのだと実感できました。
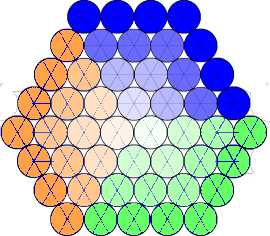
下図は、竹束問題の図を四角数3つに色分けしたものです。
小学生の頃、よく悩まされた鶴亀算は、中学に入って連立方程式を学ぶと、簡
単に解けた思い出があります。しかし、連立方程式を知らなくても鶴亀算を解くこ
とが出来ます。
今まで、算数・和算というのは、文字を使わないで巧妙に計算する術だという認
識がありました。昔の和算家は、どのような考え方をして巧妙な術を見いだしたの
か、とても不思議です。でも、その感覚は理解できます。私も小学生時代は、算数
の応用題を文字を使わないで数字だけで立式して答を出していましたから。
MM3210さんの取り組まれている研究には、大いに関心が持てました。まだ、
部分的にしか理解していないので、今後ともHPの方を読まさせていただきたいと
思います。
