僩儞僈偐傜偺乽嬻怳乿偵傛傞捗攇偺塭嬁側偳偄傠偄傠偁偭偨偑丄偲傕偁傟僥僗僩偼柍帠廔椆偟
偨丅
丂崱夞偼偩偄傇栤戣偑擄壔偟丄暯嬒揰傕丄悢妛嘥丒俙偑侾俈揰尭偺係侽揰丄惗暔偑俀俀揰尭偺
俆侽揰側偳丄奺嫵壢偱戝暆偵壓偑傞尒捠偟偩丅偨偩丄摼揰挷惍偼峴傢傟側偄傛偆偩丅僥僗僩梻
擔偺寧梛擔偼丄帺屓嵦揰偺妛峑傕懡偐偭偨傠偆丅栚昗揰悢偵撏偐側偐偭偨庴尡惗傕懡偐偭
偨偵堘偄側偄丅傎偲傫偳偺庴尡惗偼偦偆側偺偱丄婥帩偪傪憗傔偵愗傝懼偊偰丄俀師帋尡偱婃
挘偭偰梸偟偄偲婅偆丅
仈戝妛擖帋僙儞僞乕偺敪昞(2/7)偵傛傟偽丄悢妛嘥丒俙偺暯嬒揰偼慜擭搙偺俆俈丏俇俉揰偐傜俁俈丏俋俇揰
丂偵戝暆尭偵側傞偲偺偙偲偱偁傞丅偙傟偱偼庴尡惗偑偐傢偄偦偡偓傞丏丏丏丅
丂崱丄悢妛嘥丒俙偺栤戣傪挱傔偰偄偰丄嶐擭搙偺栤戣偺弌戣孹岦偐傜媽棃偺孹岦偵暅屆偟
偨傛偆側僀儊乕僕偩丅
丂柺敀偦偆側栤戣傪偄偔偮偐庢傝忋偘丄挧愴偟偨偄偲巚偆丅栤戣暥偼堦晹夵戣偱偡丅
戞係栤丂仺丂乽晄掕曽掱幃乿偵宖嵹丅
丂堷偒懕偄偰栚偵偮偄偨偺偑戞俆栤偺栤戣偱偡丅乽曈乣乿傗乽捈慄乣乿偺尵梩尛偄偵拲堄偡
傞昁梫偑偁傝傑偡偹丅
戞俆栤丂丂仮俙俛俠偺廳怱傪俧偲偟丄慄暘俙俧忋偱揰俙偲偼堎側傞埵抲偵揰俢傪偲傞丅捈慄俙俧偲
丂丂丂丂丂曈俛俠偺岎揰傪俤偲偡傞丅傑偨丄捈慄俛俠忋偱曈俛俠忋偵偼側偄埵抲偵揰俥傪偲傞丅捈
丂丂丂丂丂慄俢俥偲曈俙俛偺岎揰傪俹丄捈慄俢俥偲曈俙俠偺岎揰傪俻偲偡傞丅
乮侾乯丂揰俢偼慄暘俙俧偺拞揰偱偁傞偲偡傞丅偙偺偲偒丄仮俙俛俠偺宍忬偵娭學側偔丄俙俢/俢俤偼
丂丂堦掕偱偁傞丅俙俢/俢俤偺抣傪媮傔傛丅傑偨丄揰俥偺埵抲偵娭學側偔丄俛俹/俙俹亄俠俻/俙俻偼
丂丂堦掕偱偁傞丅俛俹/俙俹亄俠俻/俙俻偺抣傪媮傔傛丅
乮俀乯丂俙俛亖俋丄俛俠亖俉丄俙俠亖俇偲偟丄乮侾乯偲摨條偵丄揰俢偼慄暘俙俧偺拞揰偱偁傞偲偡傞丅偙
丂丂偙偱丄係揰俛丄俠丄俻丄俹偑摨堦墌廃忋偵偁傞傛偆偵揰俥傪偲傞丅偙偺偲偒丄俙俹丄俙俻丄俠俥偺
丂丂抣傪媮傔傛丅
乮俁乯丂仮俙俛俠偺宍忬傗揰俥偺埵抲偵娭學側偔丄偮偹偵俛俹/俙俹亄俠俻/俙俻亖侾侽偲側傞傛偆偵丄
丂丂俙俢/俢俧偺抣傪媮傔傛丅
乮夝乯乮侾乯丂戣堄傪傆傑偊偰恾傪彂偔偲丄
丂丂丂丂丂丂
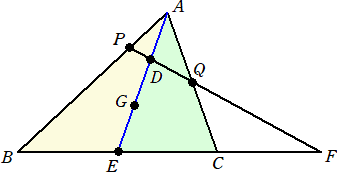
丂傑偢丄柧傜偐偵丄丂俙俢/俢俤亖侾/俀丂偱偁傞丅
丂仮俙俛俤偵偍偄偰丄儊僱儔僂僗偺掕棟傛傝丄丂乮俛俹/俙俹乯丒乮俙俢/俢俤乯丒乮俤俥/俛俥乯亖侾
丂偡側傢偪丄丂俛俹/俙俹亖俀丒乮俛俥/俤俥乯
摨條偵丄仮俙俤俠偵偍偄偰丄儊僱儔僂僗偺掕棟傛傝丄乮俠俻/俙俻乯丒乮俙俢/俢俤乯丒乮俤俥/俠俥乯亖侾
丂偡側傢偪丄丂俠俻/俙俻亖俀丒乮俠俥/俤俥乯
偙偺偲偒丄丂俛俹/俙俹亄俠俻/俙俻亖俀丒乮俛俥亄俠俥乯/俤俥亖俀丒乮俀俤俥乯/俤俥亖係
乮俀乯丂戣堄傪傆傑偊偰恾傪彂偔偲丄
丂丂丂丂丂丂
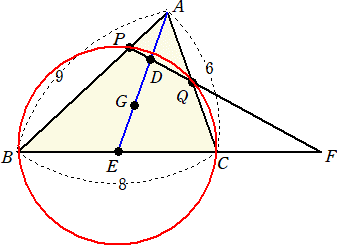
丂忋恾偵偍偄偰丄曽傋偒偺掕棟傛傝丄丂俙俹丒俋亖俙俻丒俇丂側偺偱丄丂俙俻亖乮俁/俀乯俙俹
傑偨丄乮侾乯傛傝丄丂俛俹/俙俹亄俠俻/俙俻亖係丂側偺偱丄丂俋/俙俹亄俇/俙俻亖俇丂偑惉傝棫偮丅
俙俻亖乮俁/俀乯俙俹丂傪戙擖偟偰丄丂俋/俙俹亄係/俙俹亖俇丂傛傝丄丂俙俹亖侾俁/俇
丂偙偺偲偒丄丂俙俻亖侾俁/係丂偲側傞丅
丂仮俙俛俠偵偍偄偰丄儊僱儔僂僗偺掕棟傛傝丄
丂丂乮乮侾俁/俇乯/乮係侾/俇乯乯丒乮乮俉亄俠俥乯/俠俥乯丒乮乮侾侾/係乯/乮侾俁/係乯乯亖侾
丂偡側傢偪丄乮俉亄俠俥乯/俠俥亖係侾/侾侾丂偐傜丄丂俉/俠俥亖俁侽/侾侾丂傛傝丄丂俠俥亖係係/侾俆
乮俁乯乮侾乯偲摨條偵偟偰丄
丂仮俙俛俤偵偍偄偰丄儊僱儔僂僗偺掕棟傛傝丄丂乮俛俹/俙俹乯丒乮俙俢/俢俤乯丒乮俤俥/俛俥乯亖侾
丂偡側傢偪丄丂俛俹/俙俹亖乮俢俤/俙俢乯丒乮俛俥/俤俥乯
丂仮俙俤俠偵偍偄偰丄儊僱儔僂僗偺掕棟傛傝丄乮俠俻/俙俻乯丒乮俙俢/俢俤乯丒乮俤俥/俠俥乯亖侾
丂偡側傢偪丄丂俠俻/俙俻亖乮俢俤/俙俢乯丒乮俠俥/俤俥乯
偙偺偲偒丄
丂俛俹/俙俹亄俠俻/俙俻亖乮俢俤/俙俢乯丒乮俛俥亄俠俥乯/俤俥亖乮俢俤/俙俢乯丒乮俀俤俥乯/俤俥亖俀乮俢俤/俙俢乯
丂戣堄傛傝丄丂俛俹/俙俹亄俠俻/俙俻亖侾侽丂偲側傞偨傔偵偼丄丂俢俤/俙俢亖俆丂偱偁傟偽傛偄偺偱丄
丂俙俢 丗 俢俤亖侾 丗 俆丂傛傝丄A俧 丗 俧俤亖係 丗 俀丂偱丄俙俢 丗 俢俤亖侾 丗 俁丂偲側傞丅丂丂乮廔乯
乮僐儊儞僩乯丂梊旛峑摍偺暘愅偩偲丄戞係栤偲戞俆栤偑帪娫偑偐偐傞擄栤偩偲偺偙偲偩偑丄戞係
丂丂丂丂丂丂栤偼偲傕偐偔丄戞俆栤偵偮偄偰偼丄幚嵺偵夝偄偰傒偰丄栤戣儗儀儖偲偟偰偼偦傟傎
丂丂丂丂丂丂偳偱傕側偄傛偆側丄偡偛偔慺捈側椙栤偵姶偠傞丅庴尡惗側傜偽丄庴尡栤戣廤偱宱尡偟
丂丂丂丂丂丂偰偄偦偆側暤埻婥偺栤戣偱偁傞丅
丂師偵丄戝妛擖帋僙儞僞乕偑乽廐揷夽怴曬幮偺曬摴傪嶲峫偵偟偰弌戣偟偨傕偺偱偼側偄乿偲偟
偨丄乽悢妛侾丒俙乿偺嶰妏斾偺栤戣偵挧愴偟傛偆偲巚偆丅抧忋攝旛宆寎寕僔僗僥儉攝旛傪弰傝丄
杊塹徣偺偢偝傫側挷嵏傪巜揈偟偨僗僋乕僾偲椶帡偟偰偄傞偲榖戣偵側偭偨傕偺偱偁傞丅
戞侾栤乵俀乶丂懢榊偝傫偲壴巕偝傫偼僉儍儞僾応偺僈僀僪僽僢僋偵偁傞抧恾傪尒側偑傜丄師偺傛
丂丂丂丂丂丂偆偵榖偟偰偄傞丅
懢榊丗僉儍儞僾応偺抧揰俙偐傜嶳捀俛傪尒忋偘傞妏搙偼偳傟偔傜偄偐側丅
壴巕丗抧恾傾僾儕傪巊偭偰丄抧揰俙偲嶳捀俛傪娷傓抐柺恾傪挷傋偨傜丄壓恾偺傛偆偵側偭偨傛丅
丂丂丂揰俠偼丄嶳捀俛偐傜抧揰俙傪捠傞悈暯柺偵壓傠偟偨悅慄偲偦偺悈暯柺偲偺岎揰偺偙偲偩傛丅
懢榊丗恾偺妏搙兤偼丄俙俠丄俛俠偺挿偝傪掕婯偱應偭偰丄嶰妏斾偺抣傪挷傋偨傜侾俇亱偩偭偨傛丅
壴巕丗杮摉偵侾俇亱側偺丠恾偺墧捈曽岦偺弅広偲悈暯曽岦偺弅広偼摍偟偄偺偐側丠
丂丂丂
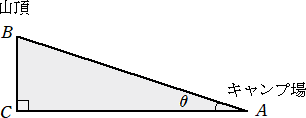
丂忋恾偺兤偼偪傚偆偳侾俇亱偱偁偭偨偲偡傞丅偟偐偟丄恾偺弅広偼丄悈暯曽岦偑侾侽枩暘偺侾偱
偁傞偺偵懳偟偰丄墧捈曽岦偼俀枩俆愮暘偺侾偱偁偭偨丅
丂幚嵺偵僉儍儞僾応偺抧揰俙偐傜嶳捀俛傪尒忋偘傞妏偱偁傞佢俛俙俠傪峫偊傞偲偒丄
倲倎値佢俛俙俠偺抣偍傛傃佢俛俙俠偺戝偒偝傪媮傔傛丅偨偩偟丄栚偺崅偝偼柍帇偟偰峫偊傞傕偺偲
偡傞丅
乮夝乯丂倲倎値佢俛俙俠亖侽丏俀俉俇俈亐係佮侽丏侽俈俀丂傛傝丄丂佢俛俙俠佮係亱
丂丂傛偭偰丄夝摎孮偐傜慖傇偲偡傟偽丄摎偼丄嘇丂偲側傞丅丂丂乮廔乯
丂丂埲壓丄岺帠拞両
丂丂丂丂丂丂丂丂丂丂丂丂丂丂
