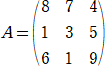
から導かれた1次変換とする。
この時、以下の基底(1)、(2)、(3)に関するFの表現行列を求めよ。
Fを行列
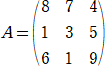
から導かれた1次変換とする。
この時、以下の基底(1)、(2)、(3)に関するFの表現行列を求めよ。
| (1) | (2) | (3) | ||
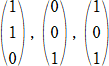 |
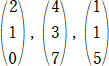 |
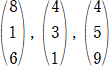 |
GAI さんからのコメントです。(令和3年11月27日付け)
多分、B1、B2、B3 が求めるものだと思います。
gp > A=[8,7,4;1,3,5;6,1,9];
gp > P1=[1,0,1;1,0,0;0,1,1];
gp > P2=[2,4,1;1,3,1;0,7,5];
gp > P3=[8,4,4;1,3,5;6,1,9];
gp > B1=P1^(-1)*A*P1
%616 =
[ 4 5 6]
[-4 10 9]
[11 -1 6]
gp > B2=P2^(-1)*A*P2
%617 =
[ 44 38 -15]
[-26 -5 21]
[ 39 25 -19]
gp > B3=P3^(-1)*A*P3
%618 =
[267/32 161/32 183/32]
[ 85/64 255/64 425/64]
[367/64 13/64 491/64]
(コメント) 懐かしい計算ですね!(1)だけやってみました。
v1=t(1 1 0) 、v2=t(0 0 1) 、v3=t(1 0 1) とおくと、v1、v2、v3 が基底
となることは明らか。(← 問題文に「基底」と書いてあるので調べる必要はないかもしれませんが、
大切なポイントなので一応確認しました!)
実際に、1次独立で、det(v1 v2 v3)=1≠0 が成り立つ。
また、標準基底として、e1=t(1 0 0) 、e2=t(0 1 0) 、e3=t(0 0 1) とおく。
このとき、行列Aの定義より、 (F(e1) F(e2) F(e3))=(e1 e2 e3)A が言える。
さらに、 v1=e1+e2 、v2=e3 、v3=e1+e3 から、底の変換行列Pは、
(v1 v2 v3)=(e1 e2 e3)P
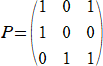
で与えられる。したがって、
(F(v1) F(v2) F(v3))
=(F(e1)+F(e2) F(e3) F(e1)+F(e3))
=(F(e1) F(e2) F(e3))P=(e1 e2 e3)AP=(v1 v2 v3)P-1AP
から、基底 v1、v2、v3 に関するFの表現行列は、P-1AP で与えられる。
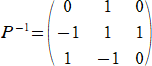
を用いて、実際に計算すると、
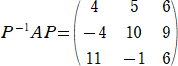
#GAI さんの計算結果と一致して、安心しました。
以下、工事中!
