をPとすると、PD（PEも）の長さが
となるのですが、皆さんならどのように計算するでしょうか？
因みに、所謂、複素数平面で、ｚ7＝１の解を用いて計算すると楽なんですけど．．．。
らすかるさんからのコメントです。（令和３年１０月１日付け）
三角関数で適当に計算してみました。
(補題) ７倍角の公式 ： cos(7θ)=64(cosθ)^7-112(cosθ)^5+56(cosθ)^3-7cosθ から、
64(cos(π/7))^7-112(cos(π/7))^5+56(cos(π/7))^3-7cos(π/7)=cosπ=-1
64(cos(π/7))^7-112(cos(π/7))^5+56(cos(π/7))^3-7cos(π/7)+1=0
{cos(π/7)+1}{8(cos(π/7))^3-4(cos(π/7))^2-4cos(π/7)+1}^2=0
ここで、cos(π/7)+1≠0なので、 8(cos(π/7))^3-4(cos(π/7))^2-4cos(π/7)+1=0
2{2cos(π/7)-1}{2(cos(π/7))^2-1}-1=0
2{2cos(π/7)-1}cos(2π/7)-1=0
4cos(π/7)cos(2π/7)-2cos(2π/7)-1=0
2cos(π/7)+2cos(3π/7)-2cos(2π/7)-1=0 （∵積和）
よって、 2{cos(π/7)+cos(3π/7)-cos(2π/7)}=1
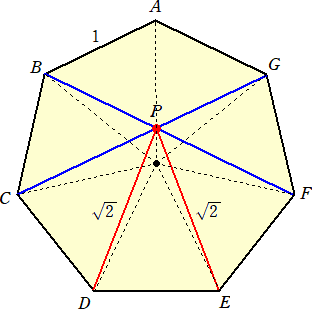
(本題) 四角形ABPGが平行四辺形であることから、
△BCPは、BC=BP=1である二等辺三角形で、∠BCP=∠BPC=2π/7
よって、CP=2cos(2π/7)
また、CD=1、∠PCD=3π/7 なので、余弦定理から、
PD^2=CD^2+CP^2-2CD・CP・cos∠PCD
=1+{2cos(2π/7)}^2-4cos(2π/7)・cos(3π/7)
=1+2{1+cos(4π/7)}-2{cos(5π/7)+cos(π/7)}
=3-2{cos(π/7)-cos(4π/7)+cos(5π/7)}
=3-2{cos(π/7)+cos(3π/7)-cos(2π/7)}
=2 （∵補題）
よって、 PD=
ＧＡＩ さんからのコメントです。（令和３年１０月１日付け）
一辺が1である正7角形の外接円の半径をRとすれば、
1=2*R^2-2*R^2*cos(2*Pi/7) から、 R=1/(2*sin(Pi/7))
1：R=sqrt(tan(Pi/7)^2/(2*sin(3*Pi/7))^2+sin(Pi/7)/sin(3*Pi/7)+1)：X から
X=｛1/(2*sin(Pi/7))｝*sqrt(tan(Pi/7)^2/(2*sin(3*Pi/7))^2+sin(Pi/7)/sin(3*Pi/7)+1)
一応、上を数値計算
gp > 1/(2*sin(Pi/7))*sqrt(tan(Pi/7)^2/(2*sin(3*Pi/7))^2+sin(Pi/7)/sin(3*Pi/7)+1)
%22 = 1.4142135623730950488016887242096980786
これの式が、sqrt(2)と同値であることは、思ってもいないですね。
gp > sqrt(2)
%23 = 1.4142135623730950488016887242096980786
ｍｏｏｎｌｉｇｈｔ さんからのコメントです。（令和３年１０月１日付け）
７倍角の公式（？）ですか！これはまた愉し気。
因みに、この話が取り交わされた界隈（出自も含めて）では、ｚ7=1の虚数解がということら
しくて、z=e^{2pi/7*i}（つまり、複素数平面上で原点中心で(1,0)を頂点に持つ正7角形の頂点）
とすると、件の線分を、z+z^2+z^4 と表わすことができると。
それで、a=z^+z^2+z^4 とすれば、a^2=(z+z^2+z^4)^2=・・・=（aの1次式） と変形できて、
aの2次方程式が得られ、それを解くことで、|a|が計算できて、それがなんと
になって、「どうなってるんだろう？」ってことで、生まれた「問題」というか「設問」のようです。
（
というサッパリした値になるということは何かあるのでは？って事でしょうか）高校の教科書に昔からある z^3=1 の虚数解ωの話の７乗版な楽しい話なのも興味を引く
点です。
「初等幾何で解く」というのも一応解決はしているのですけど、７倍角の公式の話は出てき
ませんでした。有難く面白い。（矢張り広く訊いてみるものですよね。）
それにしても、図を描いてみても思うのだけど、この長さが
になるなら、「他にもそんなことが」あるのかもとか色々考えてみたくなります。
ＧＡＩ さんからのコメントです。（令和３年１０月１日付け）
らすかるさんの解法をみて、以前関連部分を調べたことを思い出しました。
四角形ABPGが平行四辺形であることに着目して、P=cos(π/7)+cos(3π/7)-cos(2π/7)の
値 1/2 に帰着
これを以前調べたことがあり、
cos(5π/7)=cos(π-2π/7)=-cos(2π/7)から、P=cos(π/7)+cos(3π/7)+cos(5π/7)に同じ
そこで、θ1=π/7、θ2=3π/7、θ3=5π/7 と置くと、
4*θ1=π-3*θ1、4*θ2=π-3*θ2、4*θ3=π-3*θ3 より、
cos(4*θ1)=-cos(3*θ1) 、cos(4*θ2)=-cos(3*θ2) 、cos(4*θ3)=-cos(3*θ3)
即ち、どれも cos(4*θ)=-cos(3*θ) を満たす。
4倍角と3倍角の式から、 8*cos^4(θ)-8*cos^2(θ)+1=-(4*cos^3(θ)-3*cos(θ))
X=cos(θ) と置けば、 8*X^4+4*X^3-8*X^2-3*X+1=0
(X+1)*(8*X^3-4*X^2-4*X+1)=0
従って、 cos(π/7)、cos(3π/7)、cos(5π/7)は、8*X^3-4*X^2-4*X+1=0 の３根から、
根と係数の関係より、
cos(π/7)+cos(3π/7)+cos(5π/7)=cos(π/7)+cos(3π/7)-cos(2π/7)=-(-4)/8=1/2
なお、この関係式は、
cos(π/9)+cos(3*π/9)+cos(5*π/9)+cos(7*π/9)=1/2
<=> cos(2*π/9)+cos(4*π/9)+cos(6*π/9)+cos(8*π/9)=-1/2
<=> cos(π/9)-cos(2*π/9)+cos(3*π/9)-cos(4*π/9)=1/2
cos(π/11)+cos(3*π/11)+cos(5*π/11)+cos(7*π/11)+cos(9*π/11)=1/2
<=> cos(π/11)-cos(2*π/11)+cos(3*π/11)-cos(4*π/11)+cos(5*π/11)=1/2
cos(π/13)+cos(3*π/13)+cos(5*π/13)+cos(7*π/13)+cos(9*π/13)+cos(11*π/13)=1/2
以下同様。
などにも広がっていくという。
りらひいさんからのコメントです。（令和３年１０月２日付け）
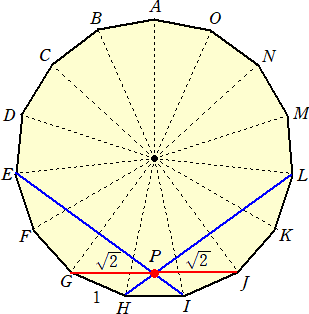
一辺の長さが1の正十五角形 ABCDEFGHIJKLMNO を考えます。この正十五角形の対角
線EIとHLの交点をPとすると、線分PG(およびPJ)の長さが
となるのですが、皆さんなら、どのように計算するでしょうか？
私は、数値計算で見つけて、比・三角関数・余弦定理などを使って確かめました。
らすかるさんからのコメントです。（令和３年１０月２日付け）
とりあえず普通に解いてみると、
GH=HI=1、∠GHP=120°、∠PHI=∠PIH=36°である四角形GHIPでGPを求めよ
という問題なので、
PH=1/(2cos36°)=(
-1)/2 より、PG^2=GH^2+PH^2-2GH・PH・cos120°=1+{(
-1)/2}^2+(-1)/2=2 から、PG=（コメント） らすかるさん、鮮やかですね！
上図の正１５角形を作図しているときに、一つの弧に対する中心角が２４°なので、その
円周角は１２°から、弧が５つ繋がれば円周角は６０°、弧が１０個繋がれば円周角は１２０°
と綺麗な性質があるんですね！普段あまり接しない正１５角形の美しい関係に触れることが
出来て感動しました。
りらひいさんからのコメントです。（令和３年１０月２日付け）
やっぱり簡単にいけますね。なんかそこそこの計算をして確かめたけれど、７のような素数
ではなくて、素因数が単純な合成数の15=3*5なので、きっと単純なはずと思って質問しました。
ありがとうございました。
以下、工事中！
