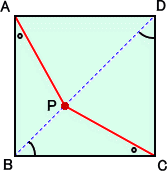
左図のような正方形ＡＢＣＤにおいて、相対する頂点 Ａ，Ｃ から、等角の線分を引く。このとき、２つの線分の交点 Ｐ
は、ちょうど正方形の対角線上にあるので、
∠ＰＢＣ＝∠ＰＤＣ
が成り立つことは明らかである。
最近、このような性質が、一般の平行四辺形においても
成り立つということを学ぶ機会があった。
左図のような平行四辺形ＡＢＣＤにおいて、辺ＢＣ、ＡＢ上にそれぞれ点Ｍ、Ｎをとり、
∠ＭＡＢ＝∠ＮＣＢ
とする。
このとき、２つの線分ＡＭ、ＣＮの交点を Ｐ
とすれば、
∠ＰＢＣ＝∠ＰＤＣ
が成り立つ。
これは自明とは言い難いので、証明が必要であろう。
（証明） まず条件より、∠ＭＡＮ＝∠ＭＣＮ なので、円周角の定理より、４点Ａ、Ｃ、Ｍ、Ｎ
は、同一円周上にある。
よって、△ＰＡＣ と △ＰＮＭ において、
∠ＰＡＣ＝∠ＰＮＭ
∠ＰＣＡ＝∠ＰＭＮ
なので、２角相等により、△ＰＡＣ ∽ △ＰＮＭ が成り立つ。
よって、 ＰＣ ： ＰＭ＝ＡＣ ： ＮＭ である。・・・・・・・・・・（*）
また、△ＡＢＣ と △ＭＢＮ において、
四角形ＡＣＭＮは、円に内接する四角形なので、 ∠ＢＡＣ＝∠ＢＭＮ で、
さらに、∠Ｂ は共通なので、２角相等により、△ＡＢＣ ∽ △ＭＢＮ が成り立つ。
よって、 ＡＣ ： ＭＮ＝ＡＢ ： ＭＢ である。・・・・・・・・・・（**）
（*）（**）により、ＰＣ ： ＰＭ＝ＡＢ ： ＭＢ＝ＣＤ ： ＭＢ が成り立つ。
このことは、△ＰＢＭ と △ＰＤＣ において、対応する２辺の比が等しいことを示す。
さらに、
∠ＰＭＢ＝∠ＰＭＮ＋∠ＮＭＢ＝∠ＰＣＡ＋∠ＣＡＢ＝∠ＰＣＡ＋∠ＡＣＤ＝∠ＰＣＤ
なので、 △ＰＢＭ ∽ △ＰＤＣ が成り立つ。
よって、 ∠ＰＢＭ＝∠ＰＤＣ が成り立つ。 （証明終）
（コメント） 最初は信じがたい結果であったが、「なるものはなる！」と納得した。それにし
ても、正方形という特殊な図形で成り立つ性質が、一般の平行四辺形でも成り
立つとは、新鮮な驚きである。
