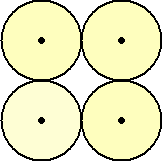
に比べて、円をずらして並べた場合
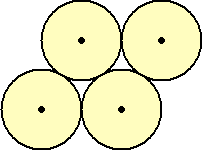
でどれくらい円の充填率は違うのだろう?興味があり、計算してみた。円の半径を1として、
円を整然と並べた場合

に比べて、円をずらして並べた場合

でどれくらい円の充填率は違うのだろう?興味があり、計算してみた。円の半径を1として、
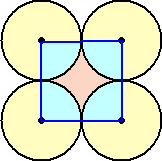 |
正方形の面積=4 扇形4個分の面積=π よって、円の充填率は、 π/4=0.7853975・・・ |
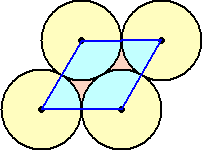 |
ひし形の面積=2×2×sin60°=2 扇形4個分の面積=π よって、円の充填率は、 π/(2 |
決まりきった定格の長方形の内部に円を詰め込む場合、上記から、円をずらして並べた
方がたくさん詰め込むことができる。
もっと充填率を上げる並べ方はあるだろうか?
Dengan kesaktian Indukmu さんからのコメントです。(令和3年8月11日付け)
上記の話題について、工学的な応用面で必要とされる問題でありながら厳密解を得難い
分野でもあり、計算機の性能向上によるヒューリスティクス解法の研究も進んでいるとのこ
とです。
(→ 参考:「正方形上への円充填問題に対するアルゴリズム」
久野誉人、佐野良夫、渡邊雅弘(筑波大学 システム情報工学研究科)
今回、ネット検索をしていて興味をひかれた問題をご紹介させてください。
問題A 一辺の長さがそれぞれ 4、2000 である長方形に敷き詰めることができる単位円
(半径が1の円)の個数は 2011 個以上であることを証明せよ。
ただし、敷き詰める円は互いに重なり合わないものとする。必要があれば、
1.9819 < √((4*√(3)) -3) < 1.982 を用いても良い。
次の問題は、初見で頭の中だけで解けてしまったという方がいて、その方のブログからで
す。私は解を知りません。商品化されて売られていたそうです。
問題B 一辺の長さがそれぞれ 10、16 である長方形に敷き詰めることができる単位円(半
径が1の円)の個数は 41 個以上であることを証明せよ。
ただし、敷き詰める円は互いに重なり合わないものとする。
らすかるさんからのコメントです。(令和3年8月11日付け)
問題Bは、14=√196>√192=8√3 だけ頭の中で計算できれば、
○○○○○
.○○○○
○○○○○
.○○○○
○○○○○
.○○○○
○○○○○
.○○○○
○○○○○
このように、41個敷き詰められることがわかりますね。
Dengan kesaktian Indukmu さんからのコメントです。(令和3年8月12日付け)
むはぁ…、全く気がつきませんでした。有り難うございます。
(コメント) らすかるさんの解を絵にまとめると、
 |
円5個の直径の和は、ぴったり10である。 左図の小正三角形の高さは、 8 で、ギリギリ16×10の長方形内に収まるんですね! らすかるさんのように、 8 とすると、エレガントかな? |
問題Aは、次のようにずらして並べていくと出来そうですね。
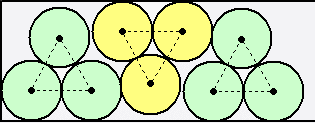
3個組みの緑色の円の右下の中心と3個組みの黄色の円の下の中心との距離をdとおく
と、三平方の定理から、
d2+(2-![]() )2=22 より、 d2=4
)2=22 より、 d2=4![]() -3 なので、問題文の注釈から、
-3 なので、問題文の注釈から、
1.9819<d<1.982
これは、中心間の距離が2から1.9819~1.982に圧縮されることを意味する。
すなわち、整然と1000個の円を並べて長さ2000となる場合に比べて、
1981.9~1982
までの長さとなり、長さ2000までまだ18~18.1の余裕があるので、もう少し円が並べら
れるというわけですね。
(追記) 令和4年7月20日付け
4年に1回開かれる国際数学連合(IMU)が、令和4年7月5日にフィールズ賞の受賞者を
発表した。
その中の一人、マリナ・ヴィヤゾフスカは、女性としては2人目の受賞で、しかも、ウウライ
ナのキーウ出身の数学者である。受賞理由は、当ページの話題をさらに一般化した
球充填問題(n次元の空間に球を詰めたときの最大密度を求める)で、8次元、24
次元を解決
とのこと。
2次元の場合は、円の半径を1として、
 |
正方形の面積=4 扇形4個分の面積=π |
とした場合は、円の充填率は、 π/4 即ち、78.5% に対して、
 |
ひし形の面積=2×2×sin60°=2 扇形4個分の面積=π |
と並べてあげると、円の充填率は、 π/(2![]() ) 即ち、 90.7% と飛躍的に向上する。
) 即ち、 90.7% と飛躍的に向上する。
上記は、2次元の場合であるが、3次元の場合は、
最密充填率は、 π/(3![]() ) 即ち、 74.0% だろう
) 即ち、 74.0% だろう
とケプラーが予想(1611年)した。
これに対して、ガウスは、1831年に、
規則正しい並びならば、最密充填率は、 π/(3![]() )
)
ということを示している。
近年になって、トーマス・C・ヘイルズが、1998年にコンピュータを使って、次のことを証明
した。
1次元の最密充填率は、 100%
2次元の最密充填率は、 90.7%
3次元の最密充填率は、 74.0%
これに対して、フィールズ賞受賞のマリナ・ヴィヤゾフスカらは、
8次元の最密充填率は、 π4/384 即ち 25.0%
24次元の最密充填率は、 π12/12! 即ち 0.19%
ということを示している。
(コメント) 8次元とか、24次元とか、想像だにできませんね...!
Dengan kesaktian Indukmu さんからのコメントです。(令和4年7月21日付け)
表題の件、是非ご紹介いたしたく存じます。
■フィールズ賞2022と符号理論|Manabu Hagiwara, 萩原学, on manau.jp
https://manau.jp/archives/4604/ (←セキュリティソフトから危険なページと判定されました!)
なお、文中にある「23次元」も「E8」も、素粒子物理学あるいは超弦理論などに使われて
いますので…… 何か関連があったら面白いのですがねえ…今のところ、そして永遠に私
のトンデモ。
ご案内したblog記事に「完全符号」なる述語が記されていました。この「完全」に多分ちょっ
とだけ関連しているオハナシを。
ホストがゲストA・ゲストBの2人とゲームをします。
●ゲームの最初の状況
ひとつの部屋があり、ホストとゲストAとがこの部屋の中に、ゲストBが部屋の外にいます。
部屋の内外は情報が遮断されています。
ホストはコインを4枚持っていて、6面体ダイスを1個持っています。ゲストはコインを1枚
持っています。
部屋にはテーブルが1台あります。テーブルの上にはよく効く眠り薬と瀬戸物の湯飲みと
があります。眠り薬は服用するとたちどころに寝てしまうしろものです。
●ゲームの第1ステップ
ゲストAの目前でホストはテーブル上でダイスをころがし1から6までの数をひとつランダム
に決めます。これをマジックナンバーと呼称することとします。
ダイスはそのまま湯飲みを被せて不可視とします。
マジックナンバーをゲストAはいつでも参照できます。(湯飲みを取り払う)
ホストは、4枚のコインについて1枚づつコイントスを行います。その順番を変えずにトスの
結果の表裏を明示しながらテーブルの上に1列にして並べます。これをコイン列と呼称する
こととします。
たとえば、 《表表裏表》 などのように。
このコイン列をゲストAは参照できます。
ゲームの第1ステップは以上です。
●ゲームの第2ステップ
ゲストAは、テーブルの上のコイン列を以下のように解釈します。
たとえば、コイン列が 《表表裏表》 であったとしたならば、 《①表②表③裏④表⑤》 と
します。
①から⑤までのどこか1箇所に限り、ゲストAは自分が持っているコインを挿入できます。
その際に、表と裏とを自由に選択できます。
たとえば、②に裏を挿入することで、 《表裏表裏表》 を得ます。これを新たなコイン列と
します。
ホストは新たなコイン列を綺麗に揃えて、どこにコインを挿入したかについては第3者には
わからなくします。
※もちろん、ホストはコインの順番を変えたり表裏をひっくり返したりしません。綺麗に揃える
だけです。
ここでゲストAは眠り薬を飲んで意識を失います。
●ゲームの第3ステップ
ゲストBが入室します。ゲストBは、テーブルの上のコイン列を参照します。その結果として、
ゲストBは、マジックナンバーを言い当てなければなりません。
言い当てればゲストAとゲストBとの勝利、言い当てられなければホストの勝利です。
以上のゲームに先立ち、ホストとゲストA、ゲストBとは、ゲームの内容、段取りについて熟
知しておくこととします。また、その上でゲストA、ゲストBとは勝利のために最良の戦術を相
談しておくことができます。
私が思うに、このゲームについて、ゲスト側に必勝法があることが、今回の投稿の冒頭で
のべた「完全」に少し関わりがあるようです。
Dengan kesaktian Indukmu さんからのコメントです。(令和4年7月27日付け)
ゲストAとゲストBとは、以下のようにダイスの目(1から6)と、5枚のコイン列の表裏の並び
とを対応づけしておきます。
―――――――――――
1 |4
赤赤黒黒赤|赤赤赤黒赤
黒赤黒黒黒|黒赤赤黒黒
黒赤赤赤赤|黒赤黒赤赤
黒黒赤黒赤|黒黒黒黒赤
|
赤黒赤赤黒|赤黒黒赤黒
―――――――――――
2 |5
赤赤黒赤黒|赤赤赤赤黒
赤黒黒黒黒|赤黒赤黒黒
赤黒赤赤赤|赤黒黒赤赤
黒黒赤赤黒|黒黒黒赤黒
|
黒赤黒黒赤|黒赤赤黒赤
―――――――――――
3 |6
赤赤黒赤赤|赤赤赤赤赤
黒黒黒黒黒|黒黒赤黒黒
赤黒黒黒赤|赤黒赤黒赤
黒赤黒赤黒|黒赤赤赤黒
|
赤赤赤黒黒|赤赤黒黒黒
黒黒赤赤赤|黒黒黒赤赤
―――――――――――
ゲストAに与えられた4枚のコイン列がどのようなものであったとしても、そこに1枚を挿入
する方法の選択肢を適宜選べば、必ず、所与のダイスの目を表す5枚のコイン列を作るこ
とができます。
