・　正方形を彫る　　 　　　　　　　　　　　　　　　　Ｓ．Ｈ氏　

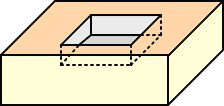
木の板に、左図のような正方形の溝を彫る必要が 　　最近起こった。彫刻刀を使ったのだが、なかなか上 　　手く彫れない。 　　　数学に、定幅曲線というのがあり、この曲線の形を 　　したドリルを使うと簡単に出来るらしい。 　　　回転しながら正方形の形が彫れるわけで、とても 　　感動的だ！

　定幅曲線とは、凸図形（図形上の２点を結ぶ線分も図形に含まれる）を任意方向の平行
線ではさみこんだとき、常にその間の距離が一定な場合を言う。

　定幅曲線の最も簡単な例は、円である。半径を ｒ とすれば、幅 ２ｒ の定幅曲線となる。

　先ほどのドリルは、次の定幅曲線をもとにして作られる。

　　　　　　　　　　


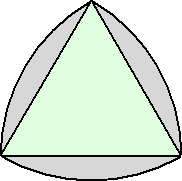
　この図形は、正三角形の各頂点で、円弧を描くことにより得られる。ルーローの三角形と
も言われ、ロータリーエンジンにも使われているらしい。

　定幅曲線であることは、簡単に確かめられる。すなわち、平行線をどのように引いても、
必ず頂点の何れかを通り、かつ、その頂点に対する弧に接する。

　正三角形の一辺の長さを、ａ とすると、ルーローの三角形の周の長さは、明らかに、

　　　　　　３×(１/６)×２πａ ＝ πａ

となる。

　一般に、定幅曲線の周の長さに関して、次の定理が知られている。

定理（バルビエ）　　幅 ｈ の定幅曲線の周の長さは、πｈ である


（参考文献：リュステルニク　著　筒井孝胤・北村辰雄　訳　凸図形と凸多面体（東京図書））


（追記）　平成１７年３月５日（土）、「世界一受けたい授業」（日本テレビ系　19:57〜20:54）
　　　　に秋山　仁　先生が登場された。先生は、いろいろな小道具を用いて、難しい数学
　　　　の話を視覚的に分かりやすく紹介してくれる。今回は、「ルーローの三角形」に関す
　　　　る話題であった。

　　　　　「マンホールは何故円形か？」の話から始まって、定幅曲線を説明し、その一つの
　　　　応用例として「ルーローの三角形」を取り上げ、それを用いて、四角形（四隅が多少
　　　　丸みを帯びているのが気になったが．．．）が彫られることを実演されていた。

　　　　　そこで、私自身一番興味を持ったのは、ルーローの５角形、７角形、９角形、・・・
　　　　の存在である。ルーローの三角形で四角形が彫られるように、ルーローの ｎ 角形で
　　　　ｎ＋１ 角形が彫られるという！
　　　　（実際の作り方は、ＨＰ：未菜実の数理パズル入門の中のこちらを参照）

　この番組を見て、定幅曲線に関する上記のバルビエの定理がすごく気になってきた。微
分幾何学の初等的知識で証明可能なようなので、このページでその証明のアウトラインを
押さえようと思う。

　高校で曲線というと、　ｙ＝Ｆ(ｘ)　という形の方程式を思い浮かべる方がほとんどだろう。
数学Ｃ を学んでいれば、媒介変数表示の　ｘ＝ｘ(ｔ)　、ｙ＝ｙ(ｔ)　の形をイメージされるかも
しれない。

　何れにしろ、平面における曲線は、なにがしかの ｘ と ｙ の関係式で与えられる。代数幾
何学では、　Ｆ( ｘ ，ｙ )＝０　という表し方が便利だが、これから考える微分幾何学では、曲
線の方程式として、媒介変数表示（パラメータ表示）

　　　　　　　　　　ｘ＝ｘ(ｔ)　、ｙ＝ｙ(ｔ)　　（ ｔ は実数）

の形の方が便利である。また、ベクトルの表現で、

　　　　　　　ｐ＝ｐ(ｔ)　　　ただし、　ｐ(ｔ)＝（ ｘ(ｔ) ， ｙ(ｔ) ）

と書くと、簡単で便利である。

　微分幾何学においては、ｘ(ｔ) 、ｙ(ｔ) が連続関数であることはもちろん、２〜３回程度は微
分可能であることを仮定する。

　ｔ で微分して、　　ｄｐ/ｄｔ＝（ ｄｘ/ｄｔ ， ｄｙ/ｄｔ ）

　さらに、ｔ で微分して、　　ｄ²ｐ/ｄｔ²＝（ ｄ²ｘ/ｄｔ² ， ｄ²ｙ/ｄｔ² ）

　ｔ を時間、ｐ を位置の関数とすれば、　ｄｐ/ｄｔ　は速度ベクトル、ｄ²ｐ/ｄｔ²　は加速度ベク
トルを表す。

　また、時間 ０ から時間 ｔ の間に点が動いた距離 ｓ は、

　　　　　　　　　　　　

により与えられる。

　距離（道のり） ｓ が 時間 ｔ の単調増加関数であるとき、時間 ｔ は距離（道のり） ｓ の関数
とも理解され、距離（道のり） ｓ を媒介変数（パラメータ）として、曲線の表示を

　　　　　　　ｐ＝ｐ(ｓ)　　　ただし、　ｐ(ｓ)＝（ ｘ(ｓ) ， ｙ(ｓ) ）

とすることができる。このとき、

　　　　　　　　　　　　｜ｄｐ/ｄｓ｜＝１

が成り立ち、曲線上を動く点の速さは、常に一定値 １ となる。

　　　　　　　ｄｐ/ｄｓ＝（ ｄｘ/ｄｓ ， ｄｙ/ｄｓ ）

において、　ｅ₁＝（ ｄｘ/ｄｓ ， ｄｙ/ｄｓ ）　とおくと、ｅ₁ は、接線方向の単位ベクトルとなる。

また、ｅ₁ を＋９０°回転したベクトルを、ｅ₂ とおく。

　ｅ₁ と ｅ₁ の内積 ｅ₁・ｅ₁＝１ であることから、両辺を ｓ で微分して、　２ｅ₁’・ｅ₁＝０

　よって、 ｅ₁’ と ｅ₂ は平行になるので、　　ｅ₁’ ＝ κ・ｅ₂　と書ける。

　この κ＝κ(ｓ) は、曲線 ｐ＝ｐ(ｓ) の曲率といわれる。曲率は、合同変換により不変である。

　この曲率の値により、曲線の曲がり具合が分かる。曲率の値が大きければ大きいほど、
曲がり方は急である。

例　曲率が恒常的に ０ な曲線は、直線に限る。

例　円の曲率は一定で、その値は半径の逆数である。（→曲率の逆数を曲率半径という。）

　　実際に、円の媒介変数表示は、　ｘ＝ｒｃｏｓ ｔ　、ｙ＝ｒｓｉｎ ｔ　　（ ｔ は実数） で、ｓ＝ｒｔ
　　　　　　よって、　ｘ＝ｒｃｏｓ（ｓ/ｒ）　、ｙ＝ｒｓｉｎ（ｓ/ｒ）
　　　　　　このとき、　ｅ₁＝（ −ｓｉｎ（ｓ/ｒ） ， ｃｏｓ（ｓ/ｒ） ）
　　　　　　　　　　　　　ｅ₂＝（ −ｃｏｓ（ｓ/ｒ） ， −ｓｉｎ（ｓ/ｒ） ）　なので、
　　　　　　　　　ｅ₁’＝（１/ｒ）（ −ｃｏｓ（ｓ/ｒ） ， −ｓｉｎ（ｓ/ｒ） ）＝（１/ｒ）ｅ₂
　　　　　　よって、　　曲率 κ＝１/ｒ　となる。

　逆に、曲率が定数 κ＞０　ならば、その曲線は半径 １/κ の円になる。

　曲線上の各点 ｐ において定まる ｅ₂ を平行移動して、始点が常に原点であるようにする。
このとき、曲線上の点 ｐ に、単位円周上の点 ｅ₂ を対応させる。この対応は通常 ｇ と表さ
れ、Ｇａｕｓｓの表示という。

　　　　　　

　点 ｐ が曲線上を速さ １ で動くとき、ｇ（ｐ）は、単位円周上を速さ κ で動く。

　平面上において、曲線 ｐ(ｓ) （ａ≦ｓ≦ｂ）が

　　　　　ｐ(ａ)＝ｐ(ｂ)　　かつ　　ｐ(ｓ₁)≠ｐ(ｓ₂)　（ａ≦ｓ₁＜ｓ₂≦ｂ）

を満たすとき、単純閉曲線であるといわれる。

　単純閉曲線により、平面は２つの領域（内部・外部）に分けられる。（Ｊｏｒｄａｎの定理）

　単純閉曲線上のどの２点を結ぶ線分も曲線の外部に出ないとき、曲線は、凸閉曲線と
呼ばれる。

　さらに、凸閉曲線の性質から、媒介変数 ｔ （０≦ ｔ ＜２π）に対して、

　　　　　　　ｅ₂＝（ ｃｏｓ ｔ ， ｓｉｎ ｔ ）

となるような曲線上の点 ｐ がただ一つ存在する。

　　　　

　ｔ＝０　から　ｔ　までの弧の長さを、ｓ とすると、ｓ は単調増加関数である。

よって、上記の媒介変数 ｔ は、ｓ の関数とみなすことができる。

　　ｅ₂＝（ ｃｏｓ ｔ ， ｓｉｎ ｔ ）　より、　ｅ₁＝（ ｓｉｎ ｔ ， −ｃｏｓ ｔ ）　なので、

　　　　　　　　　ｅ₁’＝（ｄｅ₁/ｄｔ）・（ｄｔ/ｄｓ）＝ｅ₂・（ｄｔ/ｄｓ）

　　ｅ₁’ ＝ κ・ｅ₂　より、　κ＝ｄｔ/ｄｓ　であることが分かる。

　この媒介変数 ｔ を用いると、凸閉曲線の幅 Ｗ(ｔ) が次のように定義される。

　　　　　　　　

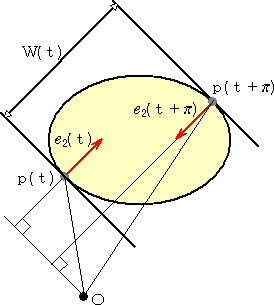
　　　　　　　Ｗ(ｔ)＝−ｐ(ｔ)・ｅ₂(ｔ)−ｐ(ｔ＋π)・ｅ₂(ｔ＋π)

　これは、ベクトル ｐ（ｔ） の ｅ₂（ｔ）方向の正射影の長さが、内積 ｐ（ｔ）・ｅ₂（ｔ） により得られる
ことから明らかであろう。（→　参考：正射影・空間の必須手法）

　このとき、凸閉曲線の長さ Ｌ は、
　　　　　　　　　　　　　　　　　　　　　　　

により与えられる。　実際に、

　　　　　　

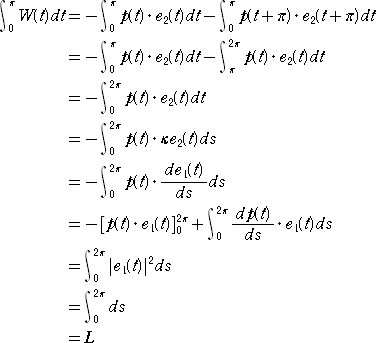
特に、幅が ｔ によらず一定値 Ｗ のとき、定幅曲線と呼ばれ、そのときの曲線の長さは、

　　　　　　　　　Ｌ＝πＷ

となる。（Ｂａｒｂｉｅｒ の定理（バルビエ）　１８６０年）

（コメント：３月５日に番組を見て興味を持って以来、解決するまで約２ヶ月、忙しかったと
　　　　　　はいえ、何とか形になり、ホッとしている．．．ｆ(^_^;) ）

（参考文献：小林昭七　著　曲線と曲面の微分幾何　（裳華房））