丂丂俙俢2亖俁2亄乮俁/俀乯2亖係俆/係 傛傝丄俙俢亖俁
丂乮俀乯丂仮俙俤俠佷仮俙俛俢丂傛傝丄
丂丂俁 丗 俁
丂乮俁乯 仮俙俫俹佷仮俙俛俢 傛傝丄倰 丗俁/俀亖俙俹 丗俁
丂側偺偱丄丂俙俹亖倰
丂曽傋偒偺掕棟傛傝丄丂倰丒乮俆亅倰乯亖倰
丂弶傔偰偺戝妛擖妛嫟捠僥僗僩偑椷榓俁擭侾寧侾俇擔丒侾俈擔偺椉擔峴傢傟偨丅戝愥偱夛応
慡懱偑墑婜偵側偭偨傝丄帋尡帪娫傪娫堘偊偰夛応偛偲墑婜偵側偭偨傝偲丄偙傟傜偼椺擭婲偙
傝偊傞帠椺偱偼偁偭偨偑丄崱擭偼夛応撪偱儅僗僋傪偢傜偟偰旲傪弌偟偰偄偨庴尡惗偑嵞嶰偺
寈崘傪柍帇偟偨偲偐偱幐奿偲側偭偨偺偼僐儘僫壭傜偟偄弌棃帠偱偁偭偨丅暿幒偵妘棧偡傟偽
嵪傓榖偱幐奿偼偄偔傜側傫偱傕尩偟偡偓側偄偩傠偆偐丠偲傕偁傟僥僗僩偼柍帠廔椆偟偨丅
丂崱丄悢妛嘥丒俙偺栤戣傪挱傔偰偄偰丄偩偄傇栤戣偺弌戣孹岦偑曄傢偭偨側偲偄偆偺偑棪捈
側姶憐偱偁傞丅
丂偦偺拞偱丄柺敀偦偆側栤戣偑師偺栤戣偱偁傞丅栤戣偑挿暥側偺偱丄堦晹徣棯偱偡丅
戞係栤丂丂墌廃忋偵侾俆屄偺揰俹0丄俹1丄丒丒丒丄俹14偑斀帪寁夞傝偵弴偵暲傫偱偄傞丅嵟弶丄
丂丂丂丂丂揰俹0偵愇偑偁傞丅
丂偝偄偙傠傪搳偘偰嬼悢偺栚偑弌偨傜愇傪斀帪寁夞傝偵俆屄愭偺揰偵堏摦偝偣丄婏悢偺栚
偑弌偨傜愇傪帪寁夞傝偵俁屄愭偺揰偵堏摦偝偣傞丅偙偺憖嶌傪孞傝曉偡丅
仈乮侾乯偼徣棯偟傑偡丅
丂嬼悢偺栚偑弌傞夞悢傪倶丄婏悢偺栚偑弌傞夞悢傪倷偲偍偔丅乮俀乯乮俁乯偼夝摎偱偡丅
乮俀乯乮俁乯丂揰俹0偵偁傞愇傪揰俹8偵堏摦偝偣傞偺偵丄帪寁夞傝偩偲丄俆倶-俁倷亖俉丂傪夝偄偰丄
丂丂倶亖4丄倷亖4丂側偺偱丄偝偄偙傠傪丂4亄4亖8乮夞乯搳偘傞昁梫偑偁傞偑丄斀帪寁夞傝偩偲丄
丂丂俆倶-俁倷亖-7傪夝偄偰丄倶亖侾丄倷亖係丂側偺偱丄偝偄偙傠傪1亄4亖俆乮夞乯搳偘傟偽傛偄丅
丂偙偙偱丄拲堄彂偒(*)偑栤戣暥偱帵偝傟偰偄傞丅
丂丂愇傪斀帪寁夞傝傑偨偼帪寁夞傝偵侾俆屄愭偺揰偵堏摦偝偣傞偲尦偺揰偵栠傞
丂偟偨偑偭偰丄揰俹0偵偁傞愇傪揰俹8偵堏摦偝偣傞偺偵搳偘傞偝偄偙傠偺夞悢偺嵟彫抣偼丄
俆夞偲側傞丅
丂埲忋傪摜傑偊偰丄栤戣偱偡丅
乮係乯丂俹1丄丒丒丒丄俹14偺偆偪偐傜揰傪堦偮慖傃丄揰俹0偵偁傞愇傪丄偝偄偙傠傪壗夞偐搳偘偰偦
丂丂偺揰偵堏摦偝偣傞丅
丂偝偄偙傠傪搳偘傞嵟彫夞悢偑嵟傕戝偒偄偺偼丄偳偺揰偵堏摦偝偣傞応崌偩傠偆偐丅
乮夝乯丂婎杮揑偵偼丄晄掕曽掱幃偺夝朄偲側傞丅
俹0仺俹1
乮斀帪寁夞傝乯丂俆倶亅俁倷亖侾丂傪夝偄偰丄丂倶亖俀丄倷亖俁丂傛傝丄偝偄偙傠傪搳偘傞夞悢偼丄
丂丂丂丂丂丂丂丂丂俀亄俁亖俆夞
乮帪寁夞傝乯丂俆倶亅俁倷亖亅侾係丂傪夝偄偰丄丂倶亖俀丄倷亖俉丂傛傝丄偝偄偙傠傪搳偘傞夞悢偼丄
丂丂丂丂丂丂丂俀亄俁亖侾侽夞
丂傛偭偰丄偝偄偙傠傪搳偘傞嵟彫夞悢偼丄丂俆夞
俹0仺俹2
乮斀帪寁夞傝乯丂俆倶亅俁倷亖俀丂傪夝偄偰丄丂倶亖侾丄倷亖侾丂傛傝丄偝偄偙傠傪搳偘傞夞悢偼丄
丂丂丂丂丂丂丂丂丂侾亄侾亖俀夞
乮帪寁夞傝乯丂俆倶亅俁倷亖亅侾俁丂傪夝偄偰丄丂倶亖侾丄倷亖俇丂傛傝丄偝偄偙傠傪搳偘傞夞悢偼丄
丂丂丂丂丂丂丂侾亄俇亖俈夞
丂傛偭偰丄偝偄偙傠傪搳偘傞嵟彫夞悢偼丄丂俀夞
俹0仺俹3
乮斀帪寁夞傝乯丂俆倶亅俁倷亖俁丂傪夝偄偰丄丂倶亖俁丄倷亖係丂傛傝丄偝偄偙傠傪搳偘傞夞悢偼丄
丂丂丂丂丂丂丂丂丂俁亄係亖俈夞
乮帪寁夞傝乯丂俆倶亅俁倷亖亅侾俀丂傪夝偄偰丄丂倶亖侽丄倷亖係丂傛傝丄偝偄偙傠傪搳偘傞夞悢偼丄
丂丂丂丂丂丂丂侽亄係亖係夞
丂傛偭偰丄偝偄偙傠傪搳偘傞嵟彫夞悢偼丄丂係夞
俹0仺俹4
乮斀帪寁夞傝乯丂俆倶亅俁倷亖係丂傪夝偄偰丄丂倶亖俀丄倷亖俀丂傛傝丄偝偄偙傠傪搳偘傞夞悢偼丄
丂丂丂丂丂丂丂丂丂俀亄俀亖係夞
乮帪寁夞傝乯丂俆倶亅俁倷亖亅侾侾丂傪夝偄偰丄丂倶亖俀丄倷亖俈丂傛傝丄偝偄偙傠傪搳偘傞夞悢偼丄
丂丂丂丂丂丂丂俀亄俈亖俋夞
丂傛偭偰丄偝偄偙傠傪搳偘傞嵟彫夞悢偼丄丂係夞
俹0仺俹5
乮斀帪寁夞傝乯丂俆倶亅俁倷亖俆丂傪夝偄偰丄丂倶亖侾丄倷亖侽丂傛傝丄偝偄偙傠傪搳偘傞夞悢偼丄
丂丂丂丂丂丂丂丂丂侾亄侽亖侾夞
乮帪寁夞傝乯丂俆倶亅俁倷亖亅侾侽丂傪夝偄偰丄丂倶亖侾丄倷亖俆丂傛傝丄偝偄偙傠傪搳偘傞夞悢偼丄
丂丂丂丂丂丂丂侾亄俆亖俇夞
丂傛偭偰丄偝偄偙傠傪搳偘傞嵟彫夞悢偼丄丂侾夞
俹0仺俹6
乮斀帪寁夞傝乯丂俆倶亅俁倷亖俇丂傪夝偄偰丄丂倶亖俁丄倷亖俁丂傛傝丄偝偄偙傠傪搳偘傞夞悢偼丄
丂丂丂丂丂丂丂丂丂俁亄俁亖俇夞
乮帪寁夞傝乯丂俆倶亅俁倷亖亅俋丂傪夝偄偰丄丂倶亖侽丄倷亖俁丂傛傝丄偝偄偙傠傪搳偘傞夞悢偼丄
丂丂丂丂丂丂丂侽亄俁亖俁夞
丂傛偭偰丄偝偄偙傠傪搳偘傞嵟彫夞悢偼丄丂俁夞
俹0仺俹7
乮斀帪寁夞傝乯丂俆倶亅俁倷亖俈丂傪夝偄偰丄丂倶亖俀丄倷亖侾丂傛傝丄偝偄偙傠傪搳偘傞夞悢偼丄
丂丂丂丂丂丂丂丂丂俀亄侾亖俁夞
乮帪寁夞傝乯丂俆倶亅俁倷亖亅俉丂傪夝偄偰丄丂倶亖俀丄倷亖俇丂傛傝丄偝偄偙傠傪搳偘傞夞悢偼丄
丂丂丂丂丂丂丂俀亄俇亖俉夞
丂傛偭偰丄偝偄偙傠傪搳偘傞嵟彫夞悢偼丄丂俁夞
俹0仺俹8
乮斀帪寁夞傝乯丂俆倶亅俁倷亖俉丂傪夝偄偰丄丂倶亖係丄倷亖係丂傛傝丄偝偄偙傠傪搳偘傞夞悢偼丄
丂丂丂丂丂丂丂丂丂係亄係亖俉夞
乮帪寁夞傝乯丂俆倶亅俁倷亖亅俈丂傪夝偄偰丄丂倶亖侾丄倷亖係丂傛傝丄偝偄偙傠傪搳偘傞夞悢偼丄
丂丂丂丂丂丂丂侾亄係亖俆夞
丂傛偭偰丄偝偄偙傠傪搳偘傞嵟彫夞悢偼丄丂俆夞
俹0仺俹9
乮斀帪寁夞傝乯丂俆倶亅俁倷亖俋丂傪夝偄偰丄丂倶亖俁丄倷亖俀丂傛傝丄偝偄偙傠傪搳偘傞夞悢偼丄
丂丂丂丂丂丂丂丂丂俁亄俀亖俆夞
乮帪寁夞傝乯丂俆倶亅俁倷亖亅俇丂傪夝偄偰丄丂倶亖侽丄倷亖俀丂傛傝丄偝偄偙傠傪搳偘傞夞悢偼丄
丂丂丂丂丂丂丂侽亄俀亖俀夞
丂傛偭偰丄偝偄偙傠傪搳偘傞嵟彫夞悢偼丄丂俀夞
俹0仺俹10
乮斀帪寁夞傝乯丂俆倶亅俁倷亖侾侽丂傪夝偄偰丄丂倶亖俀丄倷亖侽丂傛傝丄偝偄偙傠傪搳偘傞夞悢偼丄
丂丂丂丂丂丂丂丂丂俀亄侽亖俀夞
乮帪寁夞傝乯丂俆倶亅俁倷亖亅俆丂傪夝偄偰丄丂倶亖俀丄倷亖俆丂傛傝丄偝偄偙傠傪搳偘傞夞悢偼丄
丂丂丂丂丂丂丂俀亄俆亖俈夞
丂傛偭偰丄偝偄偙傠傪搳偘傞嵟彫夞悢偼丄丂俀夞
俹0仺俹11
乮斀帪寁夞傝乯丂俆倶亅俁倷亖侾侾丂傪夝偄偰丄丂倶亖係丄倷亖俁丂傛傝丄偝偄偙傠傪搳偘傞夞悢偼丄
丂丂丂丂丂丂丂丂丂係亄俁亖俈夞
乮帪寁夞傝乯丂俆倶亅俁倷亖亅係丂傪夝偄偰丄丂倶亖侾丄倷亖俁丂傛傝丄偝偄偙傠傪搳偘傞夞悢偼丄
丂丂丂丂丂丂丂侾亄俁亖係夞
丂傛偭偰丄偝偄偙傠傪搳偘傞嵟彫夞悢偼丄丂係夞
俹0仺俹12
乮斀帪寁夞傝乯丂俆倶亅俁倷亖侾俀丂傪夝偄偰丄丂倶亖俁丄倷亖侾丂傛傝丄偝偄偙傠傪搳偘傞夞悢偼丄
丂丂丂丂丂丂丂丂丂俁亄侾亖係夞
乮帪寁夞傝乯丂俆倶亅俁倷亖亅俁丂傪夝偄偰丄丂倶亖侽丄倷亖侾丂傛傝丄偝偄偙傠傪搳偘傞夞悢偼丄
丂丂丂丂丂丂丂侽亄侾亖侾夞
丂傛偭偰丄偝偄偙傠傪搳偘傞嵟彫夞悢偼丄丂侾夞
俹0仺俹13
乮斀帪寁夞傝乯丂俆倶亅俁倷亖侾俁丂傪夝偄偰丄丂倶亖俆丄倷亖係丂傛傝丄偝偄偙傠傪搳偘傞夞悢偼丄
丂丂丂丂丂丂丂丂丂俆亄係亖俋夞
乮帪寁夞傝乯丂俆倶亅俁倷亖亅俀丂傪夝偄偰丄丂倶亖俀丄倷亖係丂傛傝丄偝偄偙傠傪搳偘傞夞悢偼丄
丂丂丂丂丂丂丂俀亄係亖俇夞
丂傛偭偰丄偝偄偙傠傪搳偘傞嵟彫夞悢偼丄丂俇夞
俹0仺俹14
乮斀帪寁夞傝乯丂俆倶亅俁倷亖侾係傪夝偄偰丄丂倶亖係丄倷亖俀丂傛傝丄偝偄偙傠傪搳偘傞夞悢偼丄
丂丂丂丂丂丂丂丂丂係亄俀亖俇夞
乮帪寁夞傝乯丂俆倶亅俁倷亖亅侾丂傪夝偄偰丄丂倶亖侾丄倷亖俀丂傛傝丄偝偄偙傠傪搳偘傞夞悢偼丄
丂丂丂丂丂丂丂侾亄俀亖俁夞
丂傛偭偰丄偝偄偙傠傪搳偘傞嵟彫夞悢偼丄丂俁夞
丂埲忋偐傜丄偝偄偙傠傪搳偘傞嵟彫夞悢偑嵟傕戝偒偄偺偼丄俹0仺俹13偺応崌偱丄偦偺偲偒偺
嵟彫夞悢偼俇夞偱偁傞丅丂丂乮廔乯
乮僐儊儞僩乯丂偙傫側偵乮係乯偺寁嶼偑庤娫庢偭偰傕攝揰偼傢偢偐偵乽俆揰乿丅偳偙偲側偔棟晄恠偝
丂丂丂丂丂丂傪姶偠傞丅偦傟偲傕丄傕偭偲僄儗僈儞僩側夝朄偑偁傞偺偩傠偆偐丠傕偭偲傕栤戣偺曽
丂丂丂丂丂丂偼丄乽俹1丄丒丒丒丄俹14偺偆偪乿偲偟側偑傜丄乽俹10丄丒丒丒丄俹14乿偐傜偺俆戰偵側偭偰偄傞偺
丂丂丂丂丂丂偱丄寁嶼検嶍尭偺恊怱偱丄偙傟偟偐夝朄偑側偄偺偐傕偟傟側偄丅
丂丂丂丂丂丂丂場傒偵丄乮侾乯偺攝揰偼俀揰丄乮俀乯偺攝揰偼俉揰丄乮俁乯偺攝揰偼俆揰偱偟偨丅
丂DD++偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俁擭侾寧侾俋擔晅偗乯
丂栤戣偺暥復傪偪傖傫偲撉傓偲丄(3) 偱 5 夞偲摎偊偝偣傞偲偒偵丄乽5 屄愭偺揰偵堏摦偡傞偺
傪 4 夞傗傞偭偰丄偦傟 1 夞偱偄偄傛偹乿偲偄偆峫偊曽偱丄8-3 偲偄偆幃傪桿摫偟偰偄傑偡丅
丂偙傟傪偪傖傫偲撉傫偱桿摫偵廬偭偨恖偼丄(4) 偵偍偄偰奺揰傊偺嵟彫夞悢偼懡偔偲傕
2+4 = 6 夞偱偁傞偙偲丄偦偟偰丄6 夞偵側傞壜擻惈偑偁傞揰偼丄5*2+(-3)*2 = -2 傛傝 P13 偟
偐側偄偙偲偵婥晅偗傞偲巚偄傑偡丅
丂偦偆偡傟偽丄偁偲偼丄P13 傊偺嵟彫夞悢偑杮摉偵 6 夞側偺偐妋擣偡傞偩偗乧乧偲偄偆傛傝丄
P8 偺 5 夞偑嵟戝抣偠傖側偄帪揰偱丄栤戣傪怣偠偰乽P13乿偲乽6乿傪儅乕僋偟偪傖偭偰栤戣側偄
傫偩偲巚偄傑偡丅
丂慡懱揑偵丄僙儞僞乕帋尡傛傝傕乽慜偺栤戣偱傗偭偨寁嶼偵偳偆偄偆堄枴偑偁偭偨偺偐傪偪傖
傫偲棟夝偟側偑傜恑傔傞乿偲偄偆偙偲偑廳梫帇偝傟偰偄偰丄傎偲傫偳偺戝栤偑乽傛偔傢偐傜側偄
偗偳寁嶼偼偱偒偨乿偲偄偆偩偗偺庴尡惗偼屻敿偺榞偱媗傑傞傛偆側峔憿偵側偭偰偄偨報徾偱
偡丅
丂暰奞偱娗棟恖偝傫偺傛偆偵桿摫傪柍帇偟偰榞傪杽傔偨応崌傕懕偒偱媗傓偙偲偵偼巀斲偁傞
偲巚偄傑偡偑丄棃擭埲崀偼栤戣偑壗傪偝偣偨偄偺偐媯傒庢傞昁梫偑偁傞偲偄偆擣幆傕峀傑偭
偰偄偔偙偲偱偟傚偆丅
乮僐儊儞僩乯丂DD++偝傫偺僐儊儞僩傪攓撉偟偰丄拲堄彂偒偺乮*乯偺恀堄偑暘偐傝傑偟偨丅
丂丂丂丂丂俆亊俁亖侾俆丂傗丂亅俁亊俆亖亅侾俆丂偐傜丄倶偵偮偄偰偼丄俁偺攞悢暘丄倷偵偮偄偰偼
丂丂丂丂俆偺攞悢暘嵎偟堷偗傞偲偄偆偙偲偱偡偐丏丏丏丅
丂偩偐傜丄偝偄偙傠傪搳偘傞夞悢偼丄係亄係亖俉乮夞乯偑嵟彫偱偼側偔丄乮係亅俁乯亄係亖俆乮夞乯偑
嵟彫偵側傞傢偗偱偡偹両
丂偦偆偡傞偲丄倶 偺庢傝摼傞壜擻惈偼丄侽丄侾丄俀丂偱丄倷 偺庢傝摼傞壜擻惈偼丄侽丄侾丄俀丄俁丄係
偲側傞偺偱丄偝偄偙傠傪搳偘傞夞悢偼丄嵟戝偱傕丂俀亄係亖俇乮夞乯丂偲偄偆偙偲偵側傞丅
丂偙偺偲偒丄俆亊俀亅俁亊係亖亅俀丂傛傝丄P0 偐傜帪寁夞傝偵俀偩偗恑傫偩揰P13 偑偡偖尒偮
偐傞偲偙傠偵姶摦偟傑偡偹丅
丂忋婰偺朿戝側寁嶼偼柍梡偩偭偨偙偲偵湵慠偲偟傑偟偨丅弌戣幰偺曽偼丄偦偙偺偲偙傠傪傛偔
峫偊偰嶌栤偝傟偨傢偗偱丄弌戣幰偺恊怱乮拲堄彂偒偺乮*乯乯偵醿傟傑偟偨丅偦偟偰丄DD++偝傫
偵姶幱偟傑偡丅
丂堷偒懕偄偰栚偵偮偄偨偺偑戞俆栤偺栤戣偱偡丅壗偲側偔夰偐偟偄庯偺栤戣偱偡偹丅
戞俆栤丂丂仮俙俛俠偵偍偄偰丄俙俛亖俁丄俛俠亖係丄俙俠亖俆偲偡傞丅佢俛俙俠偺擇摍暘慄偲曈俛俠
丂丂丂丂丂偲偺岎揰傪俢偲偡傞丅
乮侾乯丂俛俢丄俙俢傪媮傔傛丅
丂傑偨丄佢俛俙俠偺擇摍暘慄偲仮俙俛俠偺奜愙墌俷偲偺岎揰偱揰俙偲偼堎側傞揰傪俤偲偡傞丅
乮俀乯丂仮俙俤俠偵拝栚偟偰丄俙俤傪媮傔傛丅
丂仮俙俛俠偺俀曈俙俛偲俙俠偺椉曽偵愙偟丄奜愙墌俷偵撪愙偡傞墌偺拞怱傪俹偲偡傞丅墌俹偺敿
宎傪 倰 偲偡傞丅偝傜偵丄墌俹偲奜愙墌偺愙揰傪俥偲偟丄捈慄俹俥偲奜愙墌俷偲偺岎揰偱揰俥偲偼
堎側傞揰傪俧偲偡傞丅
乮俁乯丂俙俹丄俹俧傪媮傔丄曽傋偒偺掕棟傪梡偄偰丄倰 傪媮傔傛丅
丂仮俙俛俠偺撪怱傪俻偲偡傞丅
乮係乯丂撪愙墌俻偺敿宎丄俙俻傪媮傔傛丅
丂傑偨丄墌俹偲曈俙俛偲偺愙揰傪俫偲偡傞丅
乮俆乯丂俙俫傪媮傔傛丅
乮俇乯丂埲忋偐傜丄揰俫偵娭偡傞師偺乮倎乯丄乮倐乯偺惓岆傪敾抐偣傛丅
丂丂乮倎乯丂揰俫偼俁揰俛丄俢丄俻傪捠傞墌偺廃忋偵偁傞丅
丂丂乮倐乯丂揰俫偼俁揰俛丄俤丄俻傪捠傞墌偺廃忋偵偁傞丅
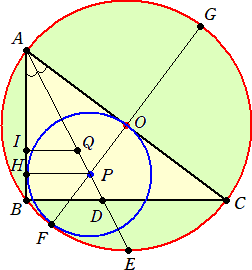
乮夝乯丂忋婰偺恾傪昤偔偺傕戝曄偦偆偱丄庤彂偒偱偼崿棎偡傞偙偲娫堘偄側偟丅忦審偵拤幚偵
丂丂丂恾傪昤偔偲丄壓恾偺傛偆偵側傞丅偙偺恾傪尒側偑傜丄夝偄偰偄偒傑偟傚偆丅
 |
丂乮侾乯丂俛俢亖係亊乮俁/俉乯亖俁/俀 丂丂俙俢2亖俁2亄乮俁/俀乯2亖係俆/係 傛傝丄俙俢亖俁 丂乮俀乯丂仮俙俤俠佷仮俙俛俢丂傛傝丄 丂丂俁 丗 俁 丂乮俁乯 仮俙俫俹佷仮俙俛俢 傛傝丄倰 丗俁/俀亖俙俹 丗俁 丂側偺偱丄丂俙俹亖倰 丂曽傋偒偺掕棟傛傝丄丂倰丒乮俆亅倰乯亖倰 |
丂傛偭偰丄俆倰亅倰2亖侾侽倰亅俆倰2丂傛傝丄丂係倰2亖俆倰丂側偺偱丄丂倰亖俆/係丂偲側傞丅
乮係乯丂撪愙墌俻偺敿宎傪 倶 偲偍偔偲丄愙慄偺挿偝偼摍偟偄偺偱丄
丂丂丂係亅乮俆亅乮俁亅倶乯乯亖倶丂傛傝丄丂倶亖侾
丂仮俙俬俻佷仮俙俛俢丂傛傝丄丂俀 丗 俁亖俙俻 丗 俁![]() /俀丂側偺偱丄丂俙俻亖
/俀丂側偺偱丄丂俙俻亖![]()
乮俆乯丂仮俙俫俹佷仮俙俛俢丂傛傝丄丂俙俫 丗 俁亖俙俹 丗 俁![]() /俀亖乮俆/係乯
/俀亖乮俆/係乯![]() 丗 俁
丗 俁![]() /俀亖俆 丗 俇
/俀亖俆 丗 俇
丂側偺偱丄丂俙俫亖俆/俀
乮俇乯丂仮俙俬俻佷仮俻俬俫丂傛傝丄丂佢俙俻俬亖佢俻俫俬丂側偺偱丄丂佢俻俫俬亖佢俻俢俛
丂丂丂墌偵撪愙偡傞巐妏宍偺媡傛傝丄丂巐妏宍俛俢俻俫偼墌偵撪愙偡傞偺偱丄乮倎乯偼惓偟偄丅
丂傑偨丄柧傜偐偵丄佢俻俫俬亗佢俻俤俛丂側偺偱丄揰俫偑俁揰俛丄俤丄俻傪捠傞墌偺廃忋偵偁傞偙
偲偼側偄偺偱丄乮倐乯偼岆傝偱偁傞丅丂丂乮廔乯
乮捛婰乯丂椷榓俁擭俀寧侾擔晅偗
丂崱搙偼丄悢妛嘦丒俛偺栤戣傪挱傔偰傒傛偆丅壗偲側偔栤戣偑悢妛俬丒俙偵斾傋偰堈偟偦偆偵姶
偠傜傟傞丅偦偺拞偱丄夝偄偰傒傛偆偲巚偭偨栤戣偑師偺栤戣偱偁傞丅偙偺栤戣偼慖戰栤戣偺
堦偮偱丄懡暘懡偔偺庴尡惗偼旔偗傞偱偁傠偆栤戣偲巚偆丅
乮栤戣偑挿暥側偺偱丄堦晹徣棯偱偡丅乯
戞俁栤丂丂偁傞崅峑偱惗搆慡堳傪懳徾偵捈慜侾廡娫偺撉彂帪娫偵偮偄偰挷嵏傪峴偭偨丅
丂丂丂丂丂侾侽侽恖偺惗搆傪柍嶌堊偵拪弌偟挷嵏偟偨偲偙傠丄慡偔撉彂傪偟側偐偭偨惗搆偑俁俇
丂丂丂丂丂恖偍傝丄撉彂帪娫偺暯嬒抣偼俀侽係暘偱偁偭偨丅崅峑慡懱偺撉彂帪娫偺曣暯嬒傪
丂丂丂丂丂倣丄曣昗弨曃嵎傪侾俆侽偲偡傞丅
乮侾乯慡偔撉彂傪偟側偐偭偨惗搆偺曣斾棪傪侽丏俆偲偡傞丅偙偺偲偒丄侾侽侽恖偺柍嶌堊昗杮偺偆
丂丂偪偱慡偔撉彂傪偟側偐偭偨惗搆偺悢傪倃偲偡傞偲丄倃偼乮丂丂丂乯偵廬偆丅
丂丂傑偨丄倃偺暯嬒乮婜懸抣乯偼乮丂丂丂乯丄昗弨曃嵎偼丄乮丂丂丂乯偱偁傞丅
乮夝乯丂戣堄傛傝丄丂俹乮倃亖倠乯亖100俠K(侽丏俆乯倠乮侽丏俆乯100-k 側偺偱丄妋棪曄悢倃偼俀崁暘晍
丂丂丂俛乮侾侽侽丆侽丆俆乯偵廬偄丄俤乮倃乯亖侾侽侽亊侽丏俆亖俆侽
丂丂丂倁乮倃乯亖侾侽侽亊侽丏俆亊侽丏俆亖俀俆丂丂傛偭偰丄冃乮倃乯亖併俀俆亖俆
乮俀乯丂昗杮偺戝偒偝侾侽侽偼廫暘偵戝偒偄偺偱丄侾侽侽恖偺偆偪慡偔撉彂傪偟側偐偭偨惗搆偺悢
丂丂偼嬤帡揑偵惓婯暘晍偵廬偆丅慡偔撉彂傪偟側偐偭偨惗搆偺曣斾棪傪侽丏俆偲偡傞偲偒丄慡偔
丂丂撉彂傪偟側偐偭偨惗搆偑俁俇恖埲壓偲側傞妋棪傪俹5偲偍偔丅俹5偺嬤帡抣傪媮傔傛丅
丂丂丂傑偨丄慡偔撉彂傪偟側偐偭偨惗搆偺曣斾棪傪侽丏係偲偡傞偲偒丄慡偔撉彂傪偟側偐偭偨惗搆
丂丂偑俁俇恖埲壓偲側傞妋棪傪俹4偲偍偔丅俹4偲俹5偺戝彫傪掕傔傛丅
乮夝乯丂拞怱嬌尷掕棟傛傝丄倃偼惓婯暘晍俶乮俆侽丆俆乯偵廬偆丅媮傔傞妋棪偼丄俹5亖俹乮倃亝俁俇乯
丂丂丂昗弨壔丂倅亖乮倃亅俆侽乯/俆傪峴偭偰丄丂俹5亖俹乮倅亝亅俀丏俉乯丂傪媮傔傟偽傛偄丅
丂丂丂俹5亖侽丏俆亅侽丏係俋俈係亖侽丏侽侽俀俇丂偲側傝丄嬤帡抣偼丄侽丏侽侽俁偵嬤偄丅
丂曣斾棪偑侽丏係偵壓偑傞偲丄俁俇恖偺慡懱偵偍偗傞妱崌偑媡偵崅傑傞偺偱丄柧傜偐偵丄
丂丂俹4亜俹5丂偱偁傞丅
乮僐儊儞僩乯丂栤戣偱偼俹5偺嬤帡抣傪摎偊傞偙偲偵側偭偰偄傞偑丄偙傟偼丄敿惍悢曗惓傪堄幆偟
丂丂丂丂丂丂偰偺偙偲偩傠偆丅敿惍悢曗惓傪峴偆偲丄媮傔傞妋棪偼丄俹5亖俹乮倃亙俁俇丏俆乯
丂丂丂丂丂丂昗弨壔丂倅亖乮倃亅俆侽乯/俆傪峴偭偰丄丂俹5亖俹乮倅亙亅俀丏俈乯丂傪媮傔傟偽丄
丂丂丂丂丂丂俹5亖侽丏俆亅侽丏係俋俇俆亖侽丏侽侽俁俇丂偲側傞丅
乮俁乯丂曣暯嬒倣偵懳偡傞怣棅搙俋俆亾偺怣棅嬫娫傪 俠1亝倣亝俠2 偲偡傞丅昗杮偺戝偒偝侾侽侽
丂丂偼廫暘戝偒偄偙偲偲丄侾廡娫偺撉彂帪娫偺昗杮暯嬒偑俀侽係丄曣昗弨曃嵎偑侾俆侽偱偁傞偙
丂丂偲傪梡偄傞丅偙偺偲偒丄俠1亄俠2丄俠2亅俠1偺抣傪媮傔傛丅
丂傑偨丄曣暯嬒倣偲俠1丄俠2偵偮偄偰丄怣棅嬫娫偺堄枴傪峫偊傟偽丄
丂乮俠1亝倣傕倣亝俠2傕惉傝棫偮偲偼尷傜側偄乯
偲側傞丅
乮夝乯丂曣暯嬒倣丄曣昗弨曃嵎侾俆侽側偺偱丄昗杮暯嬒![]() 偵偮偄偰丄
偵偮偄偰丄
丂丂丂丂丂丂丂丂丂丂俤乮![]() 乯亖倣丂丄冃乮
乯亖倣丂丄冃乮![]() 乯亖侾俆侽/併侾侽侽亖侾俆
乯亖侾俆侽/併侾侽侽亖侾俆
偑惉傝棫偪丄昗杮暯嬒![]() 偼丄昗杮偺戝偒偝偑廫暘戝偒偄偺偱丄惓婯暘晍俶乮倣丆俀俀俆乯偵廬
偼丄昗杮偺戝偒偝偑廫暘戝偒偄偺偱丄惓婯暘晍俶乮倣丆俀俀俆乯偵廬
偆傕偺偲尒側偣傞丅
丂偙偺偲偒丄怣棅搙俋俆亾偺怣棅嬫娫偼丄[俀侽係亅侾丏俋俇亊侾俆丆俀侽係亄侾丏俋俇亊侾俆]
偡側傢偪丄[侾俈係丏俇丆俀俁俁丏係]丂偱偁傞偺偱丄丂俠1亖侾俈係丏俇丄俠2亖俀俁俁丏係丂傛傝丄
丂俠1亄俠2亖係侽俉丂丄丂俠2亅俠1亖俆俉丏俉
乮係乯丂忋婰偺挷嵏偲偼撈棫偵摨條偺挷嵏傪峴偭偨丅偦偺挷嵏偵偍偗傞丄慡偔撉彂傪偟側偐偭
丂丂偨惗搆偺悢傪値偲偡傞丅値偲俁俇偺戝彫娭學偼乮丂暘偐傜側偄丂丂乯
乮俆乯丂撈帺挷嵏偵傛傞曣暯嬒倣偵懳偡傞怣棅搙俋俆亾偺怣棅嬫娫傪俢1亝倣亝俢2偲偡傞丅
丂丂偙偺偲偒丄惓偟偄傕偺偼偳傟偲偳傟偐丅
侾丏俠1亖俢1丄俠2亖俢2偑昁偢惉傝棫偮丅
俀丏俠1亙俢2傑偨偼俢1亙C2偺偳偪傜偐堦曽偺傒偑昁偢惉傝棫偮丅
俁丏俢2亙俠1傑偨偼俠2亙俢1偲側傞応崌傕偁傞丅
係丏俠2亅俠1亜俢2亅俢1偑昁偢惉傝棫偮丅
俆丏俠2亅俠1亖俢2亅俢1偑昁偢惉傝棫偮丅
俇丏俠2亅俠1亙俢2亅俢1偑昁偢惉傝棫偮丅
乮夝乯丂怣棅嬫娫偺堄枴傪峫偊偰丄丂俁丏偲俆丏
戞係栤丂丂弶崁俁丄岞嵎倫偺摍嵎悢楍傪乷倎値乸偲偟丄弶崁俁丄岞斾倰偺摍斾悢楍傪乷倐値乸偲偡傞丅
丂丂丂丂丂偨偩偟丄倫亗侽偐偮倰亗侽偲偡傞丅偝傜偵丄偙傟傜偺悢楍偑師傪枮偨偡偲偡傞丅
丂倎値倐値+1亅俀倎値+1倐値亄俁倐値+1亖侽丂乮値亖侾丄俀丄俁丄丒丒丒乯丂丒丒丒嘆
乮侾乯丂倫偲倰偺抣傪媮傔丄倎値丄倐値傪掕傔傛丅
乮夝乯丂嘆偺椉曈傪倐値偱妱偭偰丄丂倰丒倎値亅俀倎値+1亄俁倰亖侽丂偡側傢偪丄丂俀倎値+1亖倰乮倎値亄俁乯
倎値亖俁亄乮値亅侾乯丒倫丂丄倐値亖俁丒倰値-1丂傪戙擖偟偰丄丂俀乮俁亄値倫乯乯亖倰丒乮俇亄乮値亅侾乯丒倫乯丂傛傝丄
丂俇亄俀値倫亖俇倰亄倰値倫亅倰倫丂偡側傢偪丄丂乮倰亅俀乯値倫亖倰乮倫亅俇乯亄俇
丂偡傋偰偺値偱惉傝棫偮偙偲偲丄倫亗侽丂傛傝丄丂倰亖俀丂傪摼傞丅偝傜偵丄俀乮倫亅俇乯亄俇亖侽丂偐傜丄
倫亖俁丂傪摼傞丅
乮僐儊儞僩乯丂桿摫偵廬傢偢丄師偺傛偆偵夝偄偰傕傛偄丅
値亖侾丂偺偲偒丄嘆偼丄丂倎1倐2亅俀倎2倐1亄俁倐2亖侽 側偺偱丄丂俁丒俁倰亅俀丒俁乮俁亄倫乯亄俁丒俁倰亖侽
丂丂丂偡側傢偪丄丂俁倰亖俁亄倫
丂値亖俀丂偺偲偒丄嘆偼丄丂倎2倐3亅俀倎3倐2亄俁倐3亖侽 側偺偱丄
丂乮俁亄倫乯丒俁倰2亅俀乮俁亄俀倫乯丒俁倰亄俁丒俁倰2亖侽丂偡側傢偪丄丂倰倫亄俇倰亅俇亅係倫亖侽
丂倫亖俁倰亅俁丂傪戙擖偟偰丄丂俁倰2亅俁倰亄俇倰亅俇亅侾俀倰亄侾俀亖侽丂傛傝丄丂俁倰2亅俋倰亄俇亖侽
丂俁乮倰亅侾乯乮倰亅俀乯亖侽丂偐傜丄丂倰亖侾丄俀
丂倰亖侾丂偺偲偒丄丂倫亖侽丂偲側傝晄揔
丂倰亖俀丂偺偲偒丄丂倫亖俁丂偲側傝丄丂倎値亖俁亄乮値亅侾乯丒俁亖俁値丂丄倐値亖俁丒俀値-1
乮俀乯丂乷倎値乸丄乷倐値乸偺弶崁偐傜戞値崁傑偱偺榓傪丄偦傟偧傟媮傔傛丅
乮夝乯丂儼倎倠亖儼乮俁倠乯亖俁値乮値亄侾乯/俀丂丄儼倐倠亖儼俁丒俀倠-1亖俁乮俀値亅侾乯
乮俁乯丂悢楍乷倎値乸偵懳偟偰丄弶崁俁偺悢楍乷們値乸偑師傪枮偨偡偲偡傞丅
丂丂丂倎値們値+1亅係倎値+1們値亄俁們値+1亖侽丂乮値亖侾丄俀丄俁丄丒丒丒乯丂丒丒丒嘇
丂丂倎値偑惓偱偁傞偙偲偐傜丄嘇傪曄宍偟偰丄丂乮倎値亄俁乯們値+1亖係倎値+1們値丂傛傝丄
丂丂丂丂們値+1亖乮係倎値+1/乮倎値亄俁乯乯們値
丂偙偙偱丄丂倎値+1亖倎値亄俁丂偐傜丄丂們値+1亖係們値丂偲側傝丄悢楍乷們値乸偼丄岞斾係偺摍斾悢楍
偲側傞丅
乮係乯丂倯丄倳偼掕悢偱丄倯亗侽偲偡傞丅悢楍乷倐値乸偵懳偟偰丄弶崁俁偺悢楍乷倓値乸偑師傪枮偨偡偲
丂丂偡傞丅
丂丂丂倓値倐値+1亅倯倓値+1倐値亄倳倐値+1亖侽丂乮値亖侾丄俀丄俁丄丒丒丒乯丂丒丒丒嘊
丂倰亖俀丂偱偁傞偙偲偐傜丄丂俀倓値亅倯倓値+1亄俀倳亖侽丂傛傝丄丂倓値+1亖乮俀/倯乯乮倓値亄倳乯
丂偟偨偑偭偰丄悢楍乷倓値乸偑丄岞斾偑侽傛傝戝偒偔侾傛傝彫偝偄摍斾悢楍偲側傞偨傔偺昁梫廫暘
忦審偼丄
丂丂丂丂丂丂倯亜俀丂偐偮丂倳亖侽
丂丂丂丂丂丂丂丂丂丂丂丂丂丂