(1) 辺の長さが3、4、5である三角形の内心・外心・重心の3点で作られる三角形
(2) 辺の長さがa、b、cである三角形の内心・外心・重心の3点で作られる三角形
# (1)は比較的簡単です。(2)は、私は数時間かけて長大な式を地道に整理することにより
導き出しましたが、答えが結構綺麗な形になりますので、もしかしたらうまい方法がある
かも知れません。
(コメント) (1)を計算してみました。
直角三角形ABCにおいて、A(0,3)、B(4,0)、C(0,0)とすると、
内心 I (1,1) 、外心O(2,3/2) 、重心G(4/3,1)
なので、 IO=(1,1/2) 、IG=(1/3,0) より、求める三角形の面積Sは、
S=(1/2)|1・0−(1/2)(1/3)|=1/12
(2)は大変そうですね!
計算の見通しは、 OA=x 、OB=y 、OC=z とすると、
OG=(x+y+z)/3 、 OI=(ax+by+cz)/(a+b+c)
後は、S=(1/2)√(|OG|2|OI|2−(OG・OI)2) を計算するんですかね?
(2)の準備練習のために、(1)をベクトルを用いて解いてみました。
C=90°の直角三角形ABCにおいて、OA=x 、OB=y 、OC=z とすると、
y=−x 、|x|=|y|=|z|=5/2
また、 |z−x|=3 より、 |z|2−2z・x+|x|2=9
よって、 25/4−2z・x+25/4=9 より、 z・x=7/4
ここで、OG=(x+y+z)/3=z/3 、OI=(4x+3(−x)+5z)/12=(x+5z)/12
から、 |OG|=5/6 、
|OI|2=(|x|2+10z・x+25|z|2)/144=5/4
OG・OI=(z・x+5|z|2)/36=11/12
これらを S=(1/2)√(|OG|2|OI|2−(OG・OI)2) に代入して、
S=(1/2)√((25/36)(5/4)−121/144)=(1/2)√(1/36)=1/12
となり、先の結果と一致する。
# らすかるさんが「数時間かかった」という話を聞いて、(2)の計算になかなか踏み込めま
せん!
DD++さんからのコメントです。(令和2年12月31日付け)
ちゃんと証明はできていませんが、なんとなく
△IOG=(1/3)△IOH=|a-b||b-c||c-a| / (24r) ただし、Hは垂心で、r は内接円半径
になりそうな予感?
(コメント) らすかるさんの結果と一致しているそうです。美しい結果ですね。Hや内接円の
半径を使うと、綺麗に式がまとまるんですね!
DD++さんからのコメントです。(令和3年1月3日付け)
きちんと証明してみました。
辺の長さ a、b、c の向かいの頂点を A、B、C とします。△ABC の外心を O、内心を I、垂
心を H、重心を G とし、O、I、H から辺 BC に下ろした垂線の足をそれぞれ D、E、F としま
す。また、△ABC の面積を S、外接円半径を R、内接円半径を r とします。
△ABC が不等辺三角形の場合を考えます。a>b>c としても一般性を失いません。
このとき、∠B と ∠C は鋭角です。
また、∠A の二等分線は、辺 BC への垂線と中線の間にあるので、5点 B、F、E、D、C
はこの順に並びます。
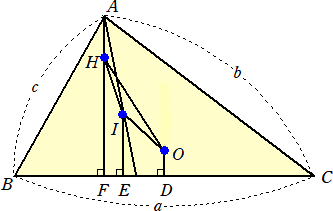
まず、点 F について。
AF = 2S/a 、BF = c*cosB = (a^2+c^2-b^2)/(2a) 、CF = b*cosC = (a^2+b^2-c^2)/(2a)
Hは垂心で、∠FBH=∠FAC などから、△BFH∽△AFC なので、
HF = BF*CF/AF = abc*cosB*cosC/(2S) = (a^2+b^2-c^2)(a^2+c^2-b^2)/(8aS)
次に、点 E について。
接線の長さの関係から、 BE = (a+c-b)/2
また、ヘロンの公式より、S^2 = (a+b+c)(a+b-c)(b+c-a)(c+a-b)/16 なので、
IE = r = 2S/(a+b+c) = (a+b-c)(b+c-a)(c+a-b)/(8S)
そして、点 D について。
BD = a/2
OD = R*cos∠BOD = (a/(2sinA))*cosA = a(b^2+c^2-a^2)/(8S)
これらを用いて、いくつかの三角形の面積を計算しておきます。
△HED
= (1/2)*HF*ED
= (1/2)*((a^2+b^2-c^2)(a^2+c^2-b^2)/(8aS))*(b-c)/2
= (b-c)(a^2+b^2-c^2)(a^2+c^2-b^2)/(32aS)
△IFD
= (1/2)*IE*FD
= (1/2)*((a+b-c)(b+c-a)(c+a-b)/(8S))*(b^2-c^2)/(2a)
= (b-c)(b+c)(a+b-c)(b+c-a)(c+a-b)/(32aS)
△OFE
= (1/2)*OD*FE
= (1/2)*(a(b^2+c^2-a^2)/(8S))*(b^2-c^2-ab+ac)/(2a)
= (b-c)a(b^2+c^2-a^2)(b+c-a)/(32aS)
さて、本題。オイラー線の性質を用いると、
△IOG = (1/3)△IOH
= (1/3)*|五角形FHIOD-四角形FHOD|
= (1/3)*|(△IHF+△IFD+△IDO)-(△HFD+△HDO)|
= (1/3)*|(△EHF+△IFD+△EDO)-(△HFD+△FDO)|
= (1/3)*|△IFD-△HED-△OFE|
= (|b-c|/(96aS))*|(b+c)(a+b-c)(b+c-a)(c+a-b)-(a^2+b^2-c^2)(a^2+c^2-b^2)-a(b^2+c^2-a^2)(b+c-a)|
となります。ここで、後ろの絶対値の中身を a の関数と考えて、
f(a) = (b+c)(a+b-c)(b+c-a)(c+a-b)-(a^2+b^2-c^2)(a^2+c^2-b^2)-a(b^2+c^2-a^2)(b+c-a)
とおくと、f(a) は a^4 の係数が -2 である四次関数で、以下の4式が成立します。
f(0) = (b+c)(b-c)(b+c)(c-b)-(b^2-c^2)(c^2-b^2) = 0
f(b) = (b+c)(2b-c)c^2-(2b^2-c^2)c^2-bc^3 = 0
f(c) = 0 (∵ f(a) は b と c の対称式なので)
f(-b-c) = (b+c)(-2c)(2b+2c)(-2b)-(2b^2+2bc)(2c^2+2bc)-(-b-c)(-2bc)(2b+2c) = 0
すなわち、因数定理より f(a) = -2a(a-b)(a-c)(a+b+c) となります。
よって、元に戻ると、
△IOG = (|b-c|/(96aS))*|-2a(a-b)(a-c)(a+b+c)| = (a+b+c)|a-b||b-c||c-a|/(48S)
となります。これに S=(1/2)r(a+b+c) を適用すれば、
△IOG = |a-b||b-c||c-a|/(24r)
となります。
以上は △ABC が不等辺三角形の場合でしたが、二等辺三角形や正三角形の場合でも、
I、O、G が同一直線上にあるとき △IOG = 0 と定義するという前提のもとであれば、この式
が成立することは明らかです。
#……うーん、計算が長い。五角形と四角形の差を思いつき、DE、EF、DF が全て (b-c) を
因数にもつことに気づき、ならば対称性から (a-b)(c-a) も出てくることを確信し、いくつかの
直角三角形での実験から分母が 24r らしいと推測して、そこまで行ってもこの計算に踏み
出すには覚悟が必要でした。
もっとエレガントな解法はあるのでしょうかね?
らすかるさんからのコメントです。(令和3年1月3日付け)
DD++さん、ありがとうございます。
私の解法は、「a、b、cで表されたIO、OG、GIを使ってヘロンの公式で求める」(たまたまIO、
OG、GIの式が手元にあったから)という強引な方法でしたので、式の整理にとんでもない手
間がかかりました。それと比較したらはるかにエレガントです。
(コメント) DD++さんの素晴らしい証明を拝見して感動しました。令和3年は素晴らしい年に
なりそうです。
