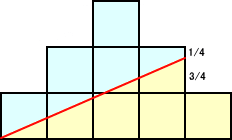
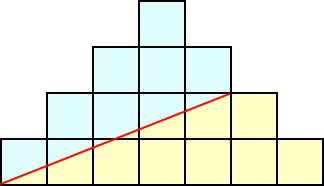
面積が１の正方形をいくつか用意します。底辺が、1、3、5、7、9、…　と対称的に山を作り、
左下角から、直線により面積を２等分します。

　ｎ段のとき、面積は、１＋３＋５＋・・・＋（２ｎ−１）＝n×n になります。

　下からの高さは、1、1、7/4、・・・ となりますが、ｎ段のときは、どうなるでしょう？


　ＧＡＩさんからのコメントです。（令和２年６月１３日付け）

　ｎが偶数のとき、　n/2

　ｎが奇数のとき、　(3*n^2+1)/(2*(3*n-1))


　ｋｓさんからのコメントです。（令和２年６月１４日付け）

　奇数と偶数に分かれるのが、不思議です。


　ｋｓさんからのコメントです。（令和２年６月１８日付け）

　奇数と偶数にわかれる公式：

　平面上の点を曲線で結ぶときの最小の交点数

　ｎが奇数のとき、　(n-1)^2(n-3)^2/64

　ｎが偶数のとき、　n(n-2)^2(n-4)/64

　他に、奇数と偶数の公式ありますか？


　らすかるさんからのコメントです。（令和２年６月１８日付け）

　奇数と偶数で場合分けされる公式はいくらでもあると思いますが、それ以前に「平面上の
点を曲線で結ぶときの最小の交点数」とは、どういう意味ですか？

　点がいくつあっても、適当な順でなぞっていけば、曲線が全く交わらないように全ての点を
結べますので、普通に考えると、「平面上の点を曲線で結ぶときの最小の交点数」は、常に
0 のような気がするのですが・・・。


　ｋｓさんからのコメントです。（令和２年６月１８日付け）

　すべて他の点と曲線でつないでの意味かなと。証明はできませんが。

例　ｎ＝５のとき、最小の交点数は、１

　　　　


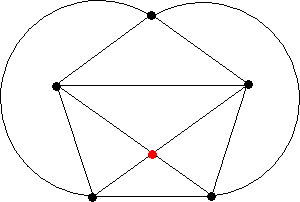
　らすかるさんからのコメントです。（令和２年６月１９日付け）

ksさんへのお返事です。

　すべて他の点と曲線でつないでの意味かなと。

　なるほど、わかりました。

　ｎが奇数のとき、　(n-1)^2(n-3)^2/64

　ｎが偶数のとき、　n(n-2)^2(n-4)/64

　この形は綺麗なので、以下のように一つにまとめることもできますね。

　(2n-1+(-1)^n)(2n-3-(-1)^n)(2n-5+(-1)^n)(2n-7-(-1)^n)/1024

　他に、例えば、

　「正n角形の頂点を結んでできる鋭角(or鈍角or直角)三角形の数」

　「n段積んだ正三角形の中に含まれる台形の個数」

なども偶奇によって場合分けしますね。


　ｋｓさんからのコメントです。（令和２年６月１９日付け）

　恐縮です。統一した式を展開したら、(ｆ＋ｇ)/2＋(−１)＾ｎ(ｆ−ｇ)/2　の形になるかなと計算
したのですが、なりませんでした。


　らすかるさんからのコメントです。（令和２年６月１９日付け）

　f(n)=n(n-2)^2(n-4)/64　、g(n)=(n-1)^2(n-3)^2/64 とすると、

　1024{f(n)+g(n)}/2=16n^4-128n^3+336n^2-320n+72

　1024{f(n)-g(n)}/2=-16n^2+64n-72

　一方、見やすくするために、(-1)^n=a　とおいて、

(2n-1+a)(2n-3-a)(2n-5+a)(2n-7-a)

=16n^4-128n^3+(-8a^2-16a+344)n^2+(32a^2+64a-352)n+(a^4+4a^3-34a^2-76a+105)

=16n^4-128n^3+(-8-16a+344)n^2+(32+64a-352)n+(1+4a-34-76a+105)　（∵a^2=1）

=16n^4-128n^3+(-16a+336)n^2+(64a-320)n+(-72a+72)

=(16n^4-128n^3+336n^2-320n+72)+a(-16n^2+64n-72)

ですから、一致しますね。