角形が最低いくつ必要か。
DD++さんからのコメントです。（令和２年５月６日付け）
3つ以下では同じ大きさの直角二等辺三角形が必要になること、5つで可能なこと（等辺が
それぞれ 4、3
、、2、2 のもので、4×6 の長方形ができる）はすぐにわかりますが、4つで可能か不可能かが難しいですね。印象的には無理っぽい感じがありますが……。
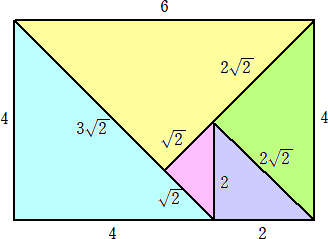
らすかるさんからのコメントです。（令和２年５月６日付け）
そうですね。難しいです。それぞれの辺に接する三角形の個数や角に集まる三角形の個
数(1か2)で地道に場合分けすれば4つでは不可能なことを示せそうな気はしますが、場合分
けが多くて大変そうです。
ところで、等辺が 4、3
、、2、2 の5つで、4×6 の他に 3×4 も作れますね。
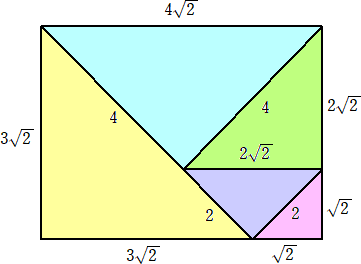
らすかるさんからのコメントです。（令和２年５月７日付け）
長方形を作るの続編として、「正方形を作る」の問題を考えました。
すべて大きさが異なるいくつかの直角二等辺三角形で正方形を作るには、直角二等辺三
角形が最低いくつ必要か。
（長方形が正方形に変わっただけですが、少し難しいです。）
スモークマンさんからのコメントです。（令和２年５月９日付け）
考えてみました ^^
正方形を異なる直角二等辺三角形5個で分割すると、内部に長方形が余り...
長方形は異なる５つの直角二等辺三角形に分割できることは言えてるので...
合計で5+5=10個 でしょうかしらん？
らすかるさんからのコメントです。（令和２年５月９日付け）
スモークマンさん、ありがとうございます。この問題も難しくて、「最小」はよくわからないの
ですが、私の「最小」は(今のところ)7個です。
スモークマンさんからのコメントです。（令和２年５月９日付け）
了解でっす♪
10、6、4x6の長方形の4をくっつけた4
にすれば、長方形内は、残り4個(3、、2、2
)なので... 3+4=7個 のものができることに気づけました ^^vらすかるさんからのコメントです。（令和２年５月９日付け）
すみません、読解力のない私には上記の意味が考えてもわかりませんので、使用する7個
の直角二等辺三角形の等辺の長さ7個を書いて頂けませんか？
（多分三角形の大きささえわかれば組み立てられるはず・・・）
スモークマンさんからのコメントです。（令和２年５月９日付け）
図がないと伝わりにくいですね...^^;
10、6、4
、3、2、2、のつもりでした...Orz
ＧＡＩさんからのコメントです。（令和２年５月９日付け）
10(A)、6(B)、4
(C)、3(D)、2(E)、2(F)、(G)と、ピースに名前をふると、一辺が10の正方形の左下から時計回りに、正方形の辺を構成
するように、A、B、E、F、Cを配置し、中に、D、Gをはめ込む感じで、隙間なく正方形が埋め
尽くされました。お見事です。
らすかるさんからのコメントです。（令和２年５月９日付け）
想定と向きが違うかもしれませんが、こんな感じですかね。（→ 図１）
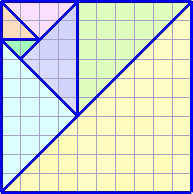
私が考えていたのは、こちらです。（→ 図２）
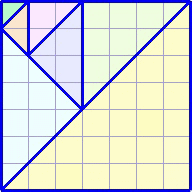
＃長方形の時に2パターンあったのがそのままこの2パターンになった感じですね。
スモークマンさんからのコメントです。（令和２年５月９日付け）
あ、上の方と同じでした♪ そっか、2通り考えられるのでしたわ...^^☆
面白かったです〜m(_ _)m〜
ＧＡＩさん、お褒めいただき恐縮です♪
長方形への埋め込み方が、あまりにも巧く見つかるものだと感心していましたので、正方
形内にその長方形を作ればと取り組んでみました ^^
長方形の分割だったら気づけなかったかもです ^^; Orz〜
ＧＡＩさんからのコメントです。（令和２年５月９日付け）
何処にも正方形をすべて敷き詰めるという但し書きが無かったので、勝手にパズル的解法
を考えてみました。
５つの直角２等辺三角形を準備：等辺の長さをそれぞれ
4、2
、4/3、4/3、2/3これらを組み合わせると、一辺が4の正方形を形作る。但し、内部に一辺が2
/3の正方形の隙間を含む。（ある意味、ここにも正方形を作れる）
