四角形ABCDがあり、AB=22、BC=16、CD=23、DA=27、AC=7 のとき、BD と 30 の大小関
係は？
　　

　ＧＡＩさんからのコメントです。（令和２年４月２３日付け）

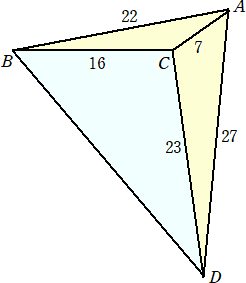
　BD=29.9999995648276105300292･･･＜30


（コメント）　∠ＢＡＣ＝α、∠ＣＡＤ＝β　とおくと、余弦定理から、

　ｃｏｓα＝（２２²＋７²−１６²）/（２・２２・７）＝２７７/３０８

　よって、　ｓｉｎα＝３{√（２０１５）}/３０８

　ｃｏｓβ＝（２７²＋７²−２３²）/（２・２７・７）＝８３/１２６

　よって、　ｓｉｎβ＝{√（８９８７）}/１２６

　以上から、

　　ＢＤ²＝２２²＋２７²−２・２２・２７・ｃｏｓ（α＋β）＝１２１３−１１８８ｃｏｓ（α＋β）

　ここで、

ｃｏｓ（α＋β）

＝ｃｏｓαｃｏｓβ−ｓｉｎαｓｉｎβ

＝（２７７/３０８）（８３/１２６）−（３{√（２０１５）}/３０８）（{√（８９８７）}/１２６）

＝（２２９９１−３√（１８１０８８０５））/３８８０８

なので、

ＢＤ²＝１２１３−３（２２９９１−３√（１８１０８８０５））/９８

　　　＝（４９９０１＋９√（１８１０８８０５））/９８＝８９９．９９９９７３８８９６５７・・・

　よって、　ＢＤ＝２９．９９９９９９５６４８２７６・・・　で、３０より小さいことが分かる。

＃ＧＡＩさんと同様の結果を得て、安心しました。


　ＧＡＩさんからのコメントです。（令和２年４月２７日付け）

　ABCDは４面体ではなく４角形なので点Cは中ではなく外にとらなければならないのでは？


（コメント）　長さに忠実に作図すると、上記のような凹四角形にならざるをえないのですが？


　らすかるさんからのコメントです。（令和２年４月２７日付け）

　Cが△ABDの内部にある場合は、四角形ABCDが「凹四角形」になるというだけのことです
ね。