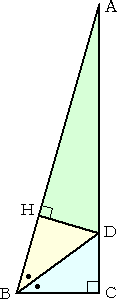
点をDとおく。このとき、 DB : BC : CD = 5 : 4 : 3 ならば、
BC : CA : AB = 7 : 24 : 25
が成り立つ。
ある意味で、一つのピタゴラス数から新しいピタゴラス数が求めら
れたわけで、とても感動的な公式である。
証明は、三平方の定理を用いる。
DB=5、BC=4、CD=3 とすると、△ADH∽△ABC から
AD=75/7 、AH=72/7 である。
(途中計算で、高校レベルの2次方程式の知識を用いる。)
・ 直角三角形の性質 S.H氏
ハンドルネーム「taku」さんという方から、直角三角形の3辺の比に関して、次のような性
質があることを教わった。
 |
左図のような △ABC において、∠Bの2等分線が辺ACと交わる 点をDとおく。このとき、 DB : BC : CD = 5 : 4 : 3 ならば、 BC : CA : AB = 7 : 24 : 25 が成り立つ。 ある意味で、一つのピタゴラス数から新しいピタゴラス数が求めら れたわけで、とても感動的な公式である。 証明は、三平方の定理を用いる。 DB=5、BC=4、CD=3 とすると、△ADH∽△ABC から AD=75/7 、AH=72/7 である。 (途中計算で、高校レベルの2次方程式の知識を用いる。) |
したがって、 AC=96/7 、AB=100/7 なので、所要の比例式の成り立つことが示さ
れる。
当HPがいつもお世話になっているHN「FN」さんが、次の形に一般化されました。
(平成23年12月23日付け)
∠Cが直角である直角三角形ABCにおいて、∠Bの2等分線と辺ACとの交点をDと
する。BC:CD=a:b (a>b>0) ならば、BC:CA:AB=a2-b2:2ab:a2+b2 であ
る。
正接の倍角の公式から容易に証明されます。
(証明) BC=a、CD=b としてよい。∠DBC=θとおくと、∠ABC=2θで、tanθ=b/a
このとき、tan2θ=2tanθ/(1-tan2θ)=2ab/(a2-b2) なので、k=a/(a2-b2) とおくと、
BC=(a2-b2)k 、AC=2abk (k>0) と書ける。三平方の定理より、
AB2=(a2-b2)2k2+4a2b2k2=(a2+b2)2k2 なので、AB=(a2+b2)k
よって、 BC:CA:AB=a2-b2:2ab:a2+b2 が成り立つ。 (証終)
a、b、c が有理数であれば、a2-b2、2ab、a2+b2 も有理数だから、1つのピタゴラス数か
ら別のピタゴラス数が得られます。
例えば、(a,b,c)=(4,3,5) とすると、上述の(7,24,25) になります。7と24を入れ替えて、
(a,b,c)=(24,7,25) として適用すると、・・・と続ければ、無限に多くのピタゴラス数が得ら
れますが、もちろん、ピタゴラス数のごく一部です。
