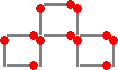
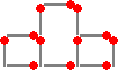
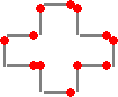
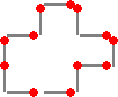
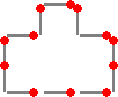
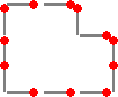
１２本のマッチ棒で、区画を作ります。一辺を１として、３〜９までの面積が作れます。それ
以外は、どうでしょう。

	面積３		面積４		面積５		面積６
	面積７		面積８		面積９

　らすかるさんからのコメントです。（令和２年４月１日付け）

　最大は、正12角形の　3(2+√3)≒11.196152　で、最小は、一辺が3のひし形をつくればいく
らでも0に近くできますので、作れる面積の範囲は、0＜(面積)≦3(2+√3)　です。

　「9が作れる」という仮定ならば、おそらく「マッチ棒を任意の角度に正確に配置できると考え
た場合に理論的に作れる値」という意味だと思いますので、整数ならば、1〜11　となります。


　ｋｓさんからのコメントです。（令和２年４月２日付け）

　有難うございます。1と2は、余った棒を、重ねてできる。10と11は、具体的にどうしたらいい
でしょう？3と4と5の三角形も面積６になりますので複数解がありますね。


　カルピスさんからのコメントです。（令和２年４月２日付け）

　これは、おそらく計算が要らない、「見た目だけで面積が、すぐに分かる」問題と解釈しま
した。

　３ｘ３＝９　の「正方形」から、１ｘ１の正方形を、角から一つづつ削っていくと、８、７、６、５
までは簡単に作れ、次に、３：４：５　の「直角三角形」を作り、面積が６なので
直角の部分から、１ｘ１＝１の正方形を、一つづつ削っていくと、５、４、３　まで作れます。

　だから、「見た目だけ分かる面積」は、私も　３、４、５、６、７、８、９　だけでした。

　面積を最大にするには「正１２角形」ですが、私には「正１２角形」の面積の求め方が分か
りませぬ．．．。

　ありゃ、ｋｓさん、「余った棒を重ねる」というのはパズルの世界では反則ではありませんか？


　ｋｓさんからのコメントです。（令和２年４月２日付け）

　重ねるというのは、四本で面積が１となる正方形を３つ作り、内部に残りを入れ並べるとい
う意味です。数学的には問題がありますが、中学入試にありました。


　DD++さんからのコメントです。（令和２年４月２日付け）

　面積1であれば、以下の方法ではどうでしょう。

　まず、マッチ棒4本で正方形を作ります。そして左右の辺のマッチ棒を取り除きます。左上
の頂点から左下の辺までマッチ棒5本で適当に折れ線を繋ぎます。右上から右下まで、左
側と平行に5本並べて繋ぎます。

　できた図形は、パッと見て面積1と判断できます。
（正方形からはみ出た部分を足りない部分に平行移動するだけ。あるいはカヴァリエリの原理）

　面積2なども含め、マッチ棒12本未満で長方形を作れれば、同様の方法でなんとかなると
思います。

．．．と思いましたが、奇数本だと他の辺と交わらないように結ぶのは難しいかも。正方形じゃ
なくても底辺1高さ1の平行四辺形ならなんでもいいので、こういう場合はほどよく傾いたものを
使ってもらうということで……。


　カルピスさんからのコメントです。（令和２年４月２日付け）

　DD++さん、ありがとうございます。なるほどー。面白い発想ですね！


　らすかるさんからのコメントです。（令和２年４月２日付け）

　面積11の作り方の例

※作成時にはマッチをたくさん使いますが、最終形で使うのは12本です。
（説明を簡単にするために座標を使います）

　マッチ9本を一直線に並べます。それぞれのマッチの座標を

　　(0,0)-(1,0)、(1,0)-(2,0)、(2,0)-(3,0)、　…　、(8,0)-(9,0)

とします。マッチを追加して、3頂点が　(0,0)、(4,0)、(0,3)　である直角三角形と3頂点が

(5,0)、(9,0)、(9,3)　である直角三角形を作ります。

(3．2,0．6)-(4,0)、(4,0)-(5,0)、(5,0)-(5．8,0．6)　の3本のマッチだけ残して、他は取り除きます。

　すると、「＼＿／」のような形になります。「＼＿／」の下底は1、上底（開放側）は2．6、高さ
は0．6、上底を線でつないで台形にした時の面積は1．08です。

　この形を4つ作り、開放側の4つの上底で正方形を作るように（全体が円形っぽくなるように）
つなげると、面積は、1．08×4+2．6^2=11．08　となり、11より少し大きくなります。

　そこで、4つの上底で作られている正方形の面積を0．08減らすように(各3本の「＼＿／」形
の角度は変えずに)少しひし形に歪ませます。

　このとき、ひし形の一辺(長さ2．6)を底辺としたときの高さが　167/65(2．6=169/65より少し
小さい)となるように歪ませれば、面積はちょうど11になります。

　この歪みを作るためには、斜辺が169、他の1辺が167である直角三角形を作れば、ひし形
の角度は作れますので、実際の手作業としても理論的に作成可能です。

　また、ひし形の高さ167/65を142/65とすれば面積は10になりますので、斜辺が169、他の
1辺が142である直角三角形を作って、ひし形の角度を決めることにより、面積10も作成可
能です。


　ｋｓさんからのコメントです。（令和２年４月２日付け）

　同じコンセプトで、三本で正三角形の面積を１として、12本で、18まで作れました。


　カルピスさんからのコメントです。（令和２年４月５日付け）

　「マッチ棒で囲む図形の面積」ですが、「面積４」は、私は、まずいと思いますが・・・。

「面積３」も少しだけ、ひっかかるけど・・・。


（コメント）　カルピスさんからのご指摘、ごもっともです。「面積３」は許せる範囲かと思います
　　　　　　が、さすがに「「面積４」は美しくないですね！

　「面積３」、「面積４」について、カルピスさんから出された図を描いてみました。

　　　　　　　　　


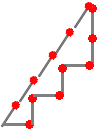
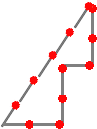
　ｋｓさんからのコメントです。（令和２年４月８日付け）

　元の問題を改題してました。マッチ棒ではなく、長さ１メートルの棒でした。それでも、現実
の棒には太さがあるので、現実には無理かも焦ら知れません。算数ならよくて、数学なら長
さ１の線分にしなくてはいけないですね。


　カルピスさんからのコメントです。（令和２年４月８日付け）

　ｋｓさんの投稿の趣旨は、冒頭の「面積４」の図に対して、内部に２本の棒が入っていますが、
数学では、「点」や「線分」は、「面積が無い」と考えるから・・・という意味ですか？


　ｋｓさんからのコメントです。（令和２年４月９日付け）

　そうですね。中にあることもそうですが。そもそも棒である限り、１メートルの四本の棒で面
積を１にすることはできないかなと思いました。角をつないで、図形を作った場合です。その
ように描いてありました。算数と数学の違いは何でしょう？


　カルピスさんからのコメントです。（令和２年４月９日付け）

　これは、ただのパズルではないのですか？？　１２本の棒で囲まれた領域が【一つの空間
になっている】が暗黙の了解事項で、冒頭の「面積３」の図は、１２本の棒を使っているけど
【三つの空間になっている】。これをルール違反にするかしないかは、パズル作問者が決め
るものだと思います。ｋｓさんの意図をくんでいない答になっていましたらスミマセン。。


　ｋｓさんからのコメントです。（令和２年４月９日付け）

　ご指摘有難うございます。中学の入試問題で、「囲まれる図形が二つ以上のものは除く」と
書かれてました。これで納得しました。