事です。もうすでに目にされた方もいるとは思いますが、もし未だの方は挑戦願う。
(よくこんな問題を考え付くもんだ!)
東京大学 前期理系(2020) 平面図形(数学A) 〜標準問題〜
2. 平面上の点P、Q、Rが同一直線上にないとき、それらを3頂点とする三角形の面積を
△PQRで表す。また、P、Q、Rが同一直線上にあるときは、△PQR=0 とする。
今、A、B、Cを平面上の3点とし、△ABC=1 とする。このとき、平面上の点Xが
2≦△ABX+△BCX+△CAX≦3
を満たしながら動くとき、Xの動きうる範囲の面積を求めよ。
らすかるさんからのコメントです。(令和2年3月23日付け)
ちゃんと図を描いたら...、多分、15/2 ですね。
スモークマンさんからのコメントです。(令和2年3月23日付け)
これが焼き直されて、2月27日に、以下のサイトで出題されてた元のものでしたのね!!
算数にチャレンジ!!第1125回問題
抽象的な表現を如何に理解・読解できるかが問われますのね...^^
GAIさんからのコメントです。(令和2年3月24日付け)
これを小学生に解かせようというわけですか。確かにその本質は比例にあるので、解いて
しまう小学生も存在するかもしれませんね。なおさら、この問題を作った人はすごい。
りらひいさんからのコメントです。(令和2年3月25日付け)
問題をちょこっと変えてみた。元の問題と比べて難しいか易しいかは微妙なところ。
平面上の点P、Q、Rが同一直線上にないとき、それらを3頂点とする三角形の面積を
△PQRで表す。また、P、Q、Rが同一直線上のあるときは、△PQR=0 とする。
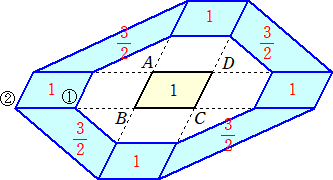
今、四角形ABCDを平面上の平行四辺形とし、その面積は 1 とする。このとき、平面上の
点Xが
2≦△ABX+△BCX+△CDX+△DAX≦3
を満たしながら動くとき、Xの動きうる範囲の面積を求めよ。
GAIさんからのコメントです。(令和2年3月25日付け)
「10」でいいんですかね?
(コメント) 見様見真似で、図を描いてみました。答えは、10で合ってるんでしょう。
DD++さんからのコメントです。(令和2年3月26日付け)
では、さらに難問をどうぞ。
空間内の点P、Q、R、Sが同一平面上にないとき、それらを4頂点とする四面体の体積を
[PQRS]で表す。(四面体記号がないので苦し紛れの記号)また、P、Q、R、Sが同一平面上
にあるときは、[PQRS]=0 とする。
今、A、B、C、Dを空間内の4点とし、[ABCD]=1 とする。このとき、空間内の点Xが
2≦[ABCX]+[BCDX]+[CDAX]+[DABX]≦3
を満たしながら動くとき、Xの動きうる範囲の体積を求めよ。
#私の計算だと46になります。第三者の結果を待ちたいところです。
りらひいさんからのコメントです。(令和2年3月26日付け)
46になりそうな気がします。証明まではできていませんが。
私が出した平行四辺形の問題は、10でいいと思います。こちらも証明していませんが…。
GAIさんからのコメントです。(令和2年3月27日付け)
全然違いますね。正直どうやったらいいのか解らなくなりました。
もう仕方ないので、A(0,0,0)、B(1,0,0)、C(0,2,0)、D(0,0,3)で、四面体[ABCD]=1 にしておき、
平面Π:x+y/2+z/3=1 すなわち、6x+3y+2z-6=0 をとり、|6x+3y+2z-6|、|x|、|y|、|z| での絶
対値を外す16通りのパターンで進んでいたんですが、もうどうしようもなくこんがらがってしま
いました。
考え直していましたが、大きく見積もっても(変な理由ですが・・・)、「22」までしか進めません
でした。
自分からは「46」というのは途轍もなく大きく感じられ、そんなにもXの存在位置があるのか
という印象です。
最も3次元を頭の中で構成しようと脳みそをフル回転させてみるんですが、如何せんパワ
ー不足です。
「46」が取り出せる思考回路を開示してもらえませんか?
DD++さんからのコメントです。(令和2年3月27日付け)
その「22」という数値が (7/8)*4+(37/8)*4 という式から来ているようであれば、もう一踏ん
張りですよ。
各辺の方向に体積4の立体が、辺の数と同じ6つだけ存在し、4*6を加えて「46」になります。
GAIさんの座標だと、
(-1/2,0,0)、(-1,0,0)、(0,-2,0)、(0,-1,0)、(-1/2,0,9/2)、(-1,0,6)、(0,-2,6)、(0,-1,9/2)
の8点を頂点とする、6つの四角形で囲まれる立体がそのうちの1つですかね。同様のものが
他にもう5つ。
GAIさんからのコメントです。(令和2年3月29日付け)
その「22」という数値が (7/8)*4+(37/8)*4 という式から来ているようであれば、
はい、この計算から求めています。
すると、上記の8点で囲まれる立体が体積4になるのですかね?その出し方が見えてきま
せん。積分で処理してみたら、2√5 になるような気もするんですが・・・
DD++さんからのコメントです。(令和2年3月29日付け)
すると、上記の8点で囲まれる立体が体積4になるのですかね?
(-1,0,0)、(0,-2,0)、(0,0,0)、(-1,0,6)、(0,-2,6)、(0,0,3) を頂点とする楔形の体積が
(1/2*1*2)*(6+6+3)/3=5
(-1/2,0,0)、(0,-1,0)、(0,0,0)、(-1/2,0,9/2)、(0,-1,9/2),(0,0,3) を頂点とする楔形の体積が
(1/2*1/2*1)*(9/2+9/2+3)/3=1
引き算して、4となりますね。
GAIさんからのコメントです。(令和2年3月29日付け)
三角柱から三角錐を取り除いたものでみればいいのか!やっと理解できました。何度も
ご教授ありがとうございました。
この部分の書き方を解釈すれば、一般に、底面が三角形で底面積をS、三角形の各頂点
での高さがh1、h2、h3であるような三角柱状の立体の体積は、3つの各高さの相加平均
(h1+h2+h3)/3を高さとする三角柱とみなして、S*(h1+h2+h3)/3で算出されると考えていいん
ですね。
DD++さんからのコメントです。(令和2年3月29日付け)
はい。このサイトでも何度か話題にあがったことがあります。四角柱状になると成立しなく
なるので、公式の使用にはかなり注意を払わないといけませんけれども。
らすかるさんからのコメントです。(令和2年3月28日付け)
2〜3の範囲をa〜bとして積分の式で書くと、
三角形の場合は、∫[a〜b]3xdx (2〜3のときは、∫[2〜3]3xdx=15/2)
平行四辺形の場合は、∫[a〜b]4xdx (2〜3のときは、∫[2〜3]4xdx=10)
のように、とても綺麗な式になりますので、四面体の場合も綺麗な式を期待したのですが、四
面体の場合は、
(3/2)∫[a〜b]5x^2-1dx (2〜3のときは、 (3/2)∫[2〜3]5x^2-1dx=46)
となり、それほど綺麗にはなりませんでした。
DD++さんからのコメントです。(令和2年3月28日付け)
私の手元では、同様に五胞体まで計算してみてあるのですが、らすかるさんの記号に揃え
て積分で書くと、
三角形の場合は ∫[a〜b](3x)dx
四面体の場合は (3/2)∫[a〜b](5x^2-1)dx
五胞体の場合は (5/2)∫[a〜b](7x^3-3x)dx
となるので、むしろ三角形の方が異質な感もあります。
5次元の六……なんていうんだろう? は流石に私の脳内じゃ無理でした。
(4次元の五胞体も絶対に合っているかと問われれば怪しいです。二次元面方向にある六胞
体の体積を求めるのが難しい……)
りらひいさんからのコメントです。(令和2年3月29日付け)
1<a≦□≦bとする。n次元単体の場合を考えたい。
私の頭では4次元以上がうまく想像できませんが、n=1、2、3の場合が次のようになるかと
思います。
※C[n,r]=n!/{r!(n-r)!}とする。
1次元単体の場合
C[2,1]*∫[(b-1)/2〜(a-1)/2]1dt/∫[-1〜0]1dt
=C[2,1]*∫[a〜b]1dx/∫[-1〜1]1dx
=∫[a〜b]1dx
2次元単体の場合
C[3,1]*∫[(b-1)/2〜(a-1)/2]tdt/∫[-1〜0](-t)dt
+ C[3,2]*∫[(b-1)/2〜(a-1)/2](t+1)dt/∫[-1〜0](t+1)dt
=C[3,1]*∫[a〜b](x-1)dx/∫[-1〜1](1-x)dx + C[3,2]*∫[a〜b](x+1)dx/∫[-1〜1](1+x)dx
=3/2*∫[a〜b](x-1)dx + 3/2*∫[a〜b](x+1)dx
=∫[a〜b]3xdx
3次元単体の場合
C[4,1]*∫[(b-1)/2〜(a-1)/2]t^2dt/∫[-1〜0](-t)^2dt
+ C[4,2]*∫[(b-1)/2〜(a-1)/2]t(t+1)dt/∫[-1〜0](-t)(t+1)dt
+ C[4,3]*∫[(b-1)/2〜(a-1)/2](t+1)^2dt/∫[-1〜0](t+1)^2dt
=C[4,1]*∫[a〜b](x-1)^2dx/∫[-1〜1](1-x)^2dx
+ C[4,2]*∫[a〜b](x-1)(x+1)dx/∫[-1〜1](1-x)(1+x)dx
+ C[4,3]*∫[a〜b](x+1)^2dx/∫[-1〜1](1+x)^2dx
=3/2*∫[a〜b](x-1)^2dx + 9/2*∫[a〜b](x-1)(x+1)dx + 3/2*∫[a〜b](x+1)^2dx
=3/2*∫[a〜b](5x^2-1)dx
以上から、n次元単体の場合は次のようになるのではないかと予想。
Σ[i=1〜n]C[n+1,i]*∫[(b-1)/2〜(a-1)/2]t^(n-i)(t+1)^(i-1)dt/∫[-1〜0](-t)^(n-i)(t+1)^(i-1)dt
=Σ[i=1〜n]C[n+1,i]*∫[a〜b](x-1)^(n-i)(x+1)^(i-1)dx/∫[-1〜1](1-x)^(n-i)(1+x)^(i-1)dx
=Σ[i=1〜n]{(n+1)*C[n,i-1]*C[n,i]/2^n}*∫[a〜b](x-1)^(n-i)(x+1)^(i-1)dx
nが偶数のとき
Σ[i=1〜n]{(n+1)*C[n,i-1]*C[n,i]/2^n}*∫[a〜b](x-1)^(n-i)(x+1)^(i-1)dx
=Σ[i=1〜n/2]{(n+1)*C[n,i-1]*C[n,i]/2^n}*∫[a〜b](x-1)^(n-i)(x+1)^(i-1)dx
+ Σ[i=n/2+1〜n]{(n+1)*C[n,i-1]*C[n,i]/2^n}*∫[a〜b](x-1)^(n-i)(x+1)^(i-1)dx
=Σ[i=1〜n/2]{(n+1)*C[n,i-1]*C[n,i]/2^n}*∫[a〜b](x-1)^(n-i)(x+1)^(i-1)dx
+ Σ[j=1〜n/2]{(n+1)*C[n,n-j]*C[n,n-j+1]/2^n}*∫[a〜b](x-1)^(j-1)(x+1)^(n-j)dx
=Σ[i=1〜n/2]{(n+1)*C[n,i-1]*C[n,i]/2^n}*∫[a〜b]{(x-1)^(n-i)(x+1)^(i-1)+(x-1)^(i-1)(x+1)^(n-i)}dx
=Σ[i=1〜n/2]{(n+1)*C[n,i-1]*C[n,i]/2^n}*∫[a〜b]{(x-1)(x+1)}^(i-1)*{(x-1)^(n-2i+1)+(x+1)^(n-2i+1)}dx
={(n+1)/2^n}*∫[a〜b]{Σ[i=1〜n/2]C[n,i-1]*C[n,i]*(x^2-1)^(i-1)*((x-1)^(n-2i+1)+(x+1)^(n-2i+1))}dx
nが奇数のとき
Σ[i=1〜n]{(n+1)*C[n,i-1]*C[n,i]/2^n}*∫[a〜b](x-1)^(n-i)(x+1)^(i-1)dx
=Σ[i=1〜(n-1)/2]{(n+1)*C[n,i-1]*C[n,i]/2^n}*∫[a〜b]{(x-1)(x+1)}^(i-1)*{(x-1)^(n-2i+1)+(x+1)^(n-2i+1)}dx
+ {(n+1)*C[n,(n+1)/2-1]*C[n,(n+1)/2]/2^n}*∫[a〜b](x-1)^(n-(n+1)/2)(x+1)^((n+1)/2-1)dx
=Σ[i=1〜(n-1)/2]{(n+1)*C[n,i-1]*C[n,i]/2^n}*∫[a〜b]{(x-1)(x+1)}^(i-1)*{(x-1)^(n-2i+1)+(x+1)^(n-2i+1)}dx
+ {(n+1)*C[n,(n-1)/2]*C[n,(n+1)/2]/2^n}*∫[a〜b]{(x-1)(x+1)}^((n-1)/2)dx
={(n+1)/2^n}*∫[a〜b]{C[n,(n-1)/2]*C[n,(n+1)/2]*(x^2-1)^((n-1)/2)
+Σ[i=1〜(n-1)/2]C[n,i-1]*C[n,i]*(x^2-1)^(i-1)*((x-1)^(n-2i+1)+(x+1)^(n-2i+1))}dx
◇もう少し計算を進められそうですが、私はうまくまとめられる自信がありません。
一応、これに n=4 を代入すると、DD++さんの答えと一致し、n=5は (15/8)∫[a〜b](21x^4-14x^2+1)dx
となりますが、この予想はどうなんでしょう??
DD++さんからのコメントです。(令和2年3月31日付け)
その積分であってそうに思います。うーん、そこまで綺麗な感じにはならないのか……。
