x、y、z を座標とする空間において、x-z平面内の曲線 z=sqrt(log(1+x)) (0≦x≦1) を、z軸
のまわりに1回転させるとき、この曲線が通過した部分よりなる図形をSとする。
このSをさらに、x軸のまわりに1回転させるとき、Sが通過した部分よりなる立体をVとする。
このとき、Vの体積を求めよ。
一晩考え続けてあれこれ挑戦していたんですが、どうしても正解に辿り着けませんでした。
解答を読んでも今一つ図形のイメージと処理の仕方がつかめずにいます。何方か、求め方
をどの様に進めるのか見せて下さい。
らすかるさんからのコメントです。(令和2年3月20日付け)
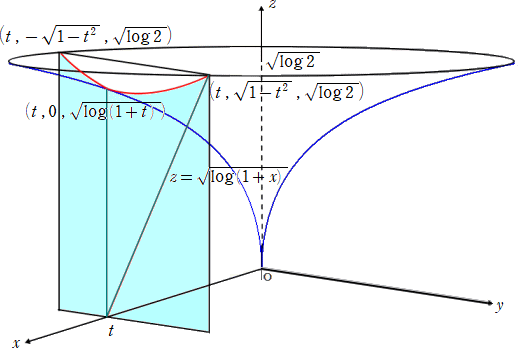
Sの上端(zが最大の部分)は、z=√log2、x^2+y^2=1ですよね。すると、x=t のときの点は、
(t,±√(1-t^2),√log2)
なので、x軸までの距離は、√(1-t^2+log2)
よって、Vは、
z=√log(1-x) (-1≦x≦0) と z=√log(1+x) (0≦x≦1) と z=√(1-x^2+log2)
で囲まれたイチョウの葉の形の面を、x軸に関して回転させた立体となり、
2π∫[0〜1](1-x^2+log2)-log(1+x) dx
=2π[x-x^3/3+xlog2-(1+x)log(1+x)+x][0〜1]
=2π(5/3-log2)
となると思います。
(コメント) 出題分野は、積分法(数学III)で、予備校の評価は「やや難」だそうです。図を見
ると、何を求めるのかが明らかになるかな?