ｙ＝ｘ²上に３点P(ｐ，ｐ²)、Q(ｑ，ｑ²)、R(ｒ，ｒ²)　（ただし、ｒ＜ｐ＜ｑ) がある。

　　

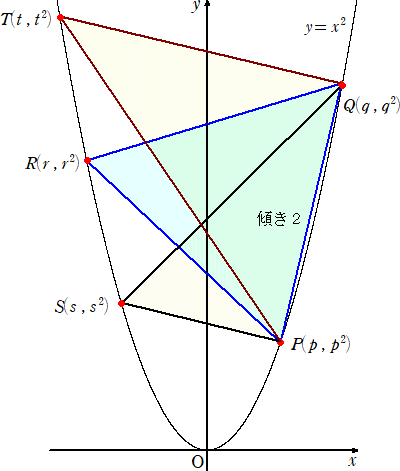
（１）　直線PQの傾きが２で、△PQRが正三角形をなしているとき、その三角形の面積S₁は？

　また、このとき、放物線上の点S(ｓ，ｓ²)　（ただし、ｒ＜ｓ＜ｐ）を適当に選ぶ。

（２）　△PQSが∠SPQ＝９０°である直角三角形であるようにしたとき、直角三角形PQSの
　　面積S₂は？

　更に、点T(ｔ，ｔ²)　（ただし、ｔ＜ｒ)を適当に選ぶ。

（３）　△PQTが∠PQT＝９０°である直角三角形であるようにしたとき、直角三角形PQTの
　　面積S₃は？


　なつさんからのコメントです。（令和２年２月２４日付け）

　神戸大かなんかで似たような問題があった気がします。ｐ＋ｑ＝２であることから、適当に
式変形をすると、ｒが求まり、いろいろやってたら、ｐとｑが求まりました。

　ｙ＝ｘ²上の３点が正三角形になるときの重心の軌跡が放物線だったりと、いろいろ面白い
事柄が隠れてそうですね…。

　何か面白い関係とかがあったら教えていただけるとありがたいです。


　ＧＡＩ さんからのコメントです。（令和２年２月２４日付け）

　２０１５年長崎大学（工学部）に、PQの傾きが１の場合であったものを傾き２で解いてみた
ものを元に出題していました。

　やり方はご指摘の方針でできますが、計算が格段に面倒になりましたが力ずくで求められ

　　S₁=375/121*　、S₂=125/44*-375/121　、S₃=125/44*+375/121

の結果になりました。
（グラフソフトで合っていそうな気もするのですが、確認したかったので、どなたかに解いても
らいたく出題しておりました。）

　なお、傾き１での正三角形と傾き２での正三角形の面積比は、　125：242＝5^3：2*11^2
でしたが、他の放物線ではどう変化するのかな？


　りらひいさんからのコメントです。（令和２年２月２５日付け）

　放物線はすべて相似であるので、二つの放物線で同じ傾きの正三角形を作れば、得られ
る正三角形は放物線を含めた一体として相似となり、二種の傾きの正三角形の面積比は
放物線を変えても変わらない気がします。

　それはそれとして、解くのにだいぶ時間がかかってしまったけれど、S₁のみ計算してみま
した。

　ｙ＝ｘ²は下に凸なので、ｒ＜ｐ＜ｑより点Pは直線QRの下側にあり、三角形PQRの頂点は
P、Q、Rの順に反時計回りとなる。

　PQの傾きを、tanθ=a とする。

QRの傾きは、tan(θ+2π/3)={tanθ+tan(2π/3)}/{1-tanθtan(2π/3)}=(a-)/(1+a)

RPの傾きは、tan(θ+4π/3)={tanθ+tan(4π/3)}/{1-tanθtan(4π/3)}=(a+)/(1-a)

　また、傾きを計算すると、PQの傾きはｐ＋ｑ、QRの傾きはｑ＋ｒ、RPの傾きはｒ＋ｐ となる
ので、

　p+q = a　、q+r = (a-)/(1+a)　、r+p = (a+)/(1-a)

　3式を足し合わせて2で割ると、

p+q+r = {a-3a^3+4a-*(1+a^2)+4a+*(1+a^2)}/{2(1-3a^2)} = {3a(3-a^2)}/{2(1-3a^2)}

よって、

　p = {3a(3-a^2)-8a+2*(1+a^2)}/{2(1-3a^2)}=a/2+*(1+a^2)/(1-3a^2)

　q = {3a(3-a^2)-8a-2*(1+a^2)}/{2(1-3a^2)}=a/2-*(1+a^2)/(1-3a^2)

　r = {3a(3-a^2)-2a+6a^3)}/{2(1-3a^2)}=a(7+3a^2)/{2(1-3a^2)}

　正三角形の一辺の長さは、

|q-p|*√(1+a^2) = {2*(1+a^2)/|1-3a^2|}*√(1+a^2) = 2*(1+a^2)*√(1+a^2)/|1-3a^2|

|r-q|*√{1+(a-)^2/(1+a)^2} = {*(1+a^2)*|1+a|/|1-3a^2|}*{2√(1+a^2)/|1+a|}
　　　　　　　　　　　　　　　　　　　　　= 2*(1+a^2)*√(1+a^2)/|1-3a^2|

|p-r|*√{1+(a+)^2/(1-a)^2} = {*(1+a^2)*|1-a|/|1-3a^2|}*{2√(1+a^2)/|1-a|}
　　　　　　　　　　　　　　　　　　　　　= 2*(1+a^2)*√(1+a^2)/|1-3a^2|

　正三角形の面積は、

　　　/4*{2*(1+a^2)*√(1+a^2)/|1-3a^2|}^2 = 3*(1+a^2)^3/(1-3a^2)^2

　ｐ、ｑ、ｒ の大小を比較すると、

　a＜-1/ のとき、p＜q＜r

　-1/＜a＜1/ のとき、q＜r＜p

　1/＜a のとき、r＜p＜q

となるので、r＜p＜q となるためには、a＞1/ が必要である。

　a=2を代入して、　S₁ = 3*(1+2^2)^3/(1-3*2^2)^2 = 375/121


（コメント）　正三角形の面積の問題は、２００４（平成１６）年度東大前期理系で出題されてい
　　　　　　ますね。なつさんのコメントにもある通り、

　１つの辺の傾きを与えれば、３つの頂点の座標をすべてその傾きで表せる

ことが解法のポイントのようです。

　ここでは、その解答の方針によらない解答を（１）についてでっち上げてみました。

　ＰＱの傾き＝ｐ＋ｑ＝２＝ｔａｎθ　、ＱＲの傾き＝ｑ＋ｒ＝ｔａｎφ　、ＲＰの傾き＝ｒ＋ｐ＝ｔａｎτ

とし、ＰＱ＝ａ　とおく。このとき、φ＝θ−π/３　、τ＝θ＋π/３　である。

　正接の加法定理により、

　ｑ＋ｒ＝ｔａｎφ＝ｔａｎ（θ−π/３）＝（２−）/（１＋２）＝（５−８）/１１

　ｒ＋ｐ＝ｔａｎτ＝ｔａｎ（θ＋π/３）＝（２＋）/（１−２）＝−（５＋８）/１１

なので、　ｑ−ｐ＝１０/１１

　ところで、　ａ＝（ｑ−ｐ）　なので、　ａ＝（１０/１１）√１５

　したがって、　S₁＝（/４）ａ²＝（３７５/１２１）


＃ＧＡＩさんの結果と一致して安心しました。面積の計算には関係なさそうですが、

　ｑ＋ｒ＝（５−８）/１１、ｒ＋ｐ＝−（５＋８）/１１　から、辺々加えて、

　２ｒ＋２＝−１６/１１　から、　ｒ＝−１９/１１　とｒが求まり、そこから、ｐ、ｑも求められますね。


　りらひいさんからのコメントです。（令和２年２月２５日付け）

　60°回転のほうが楽かと思ったけど、そうでもなかった……。

　放物線を複素平面上におく。点Rは点Pを中心として点Qを反時計回りに60°回転した点
なので、

r+ir^2
= (p+ip^2) + {(q+iq^2)-(p+ip^2)} * {(1+i)/2}
= (p+ip^2) + (q-p)*{1+i(p+q)}*(1+i)/2
= (p+ip^2) + (q-p)*{1-(p+q)+i(p+q+)}/2
= {p+q-(p+q)(q-p)+i(p^2+q^2+(q-p))}/2
= (p+q){1-(q-p)}/2 + i{p^2+q^2+(q-p)}/2

　実部と虚部を比較して、　r=(p+q){1-(q-p)}/2　、r^2={p^2+q^2+(q-p)}/2

よって、
0
= (p+q)^2*{1-(q-p)}^2 - 2*{p^2+q^2+(q-p)}
= (p+q)^2*{1+3(q-p)^2-2(q-p)} - {(p+q)^2+(q-p)^2+2(q-p)}
= (q-p) * {(q-p)*(3(p+q)^2-1) - 2*((p+q)^2+1)}

　P、Qは異なる点で、q-p≠0　なので、　q-p = 2*{(p+q)^2+1}/{3(p+q)^2-1}

PQの長さは、

√{(q-p)^2+(q^2-p^2)^2}
= |q-p|*√{1+(p+q)^2}
=  2*{(p+q)^2+1}*√{(p+q)^2+1}/|3(p+q)^2-1|

　正三角形PQRの面積は、

/4 * [2*{(p+q)^2+1}*√{(p+q)^2+1}/|3(p+q)^2-1|]^2
=3*{(p+q)^2+1}^3/{3(p+q)^2-1}^2

　ここで、PQの傾きは、p+qとなることに注意する。p+q=2　を代入すると、面積は、

　3*{2^2+1}^3/{3*2^2-1}^2 = 375√3/121


　らすかるさんからのコメントです。（令和２年２月２６日付け）

S₁：　ｙ＝ｘ²をPが原点になるように平行移動して、ｙ＝ｘ²＋ａｘ　とおく。

　点(2，4)を原点中心として反時計回りに60°回転した点は、(1-2，2+)なので、

Q(2b，4b)、R((1-2)b，(2+)b)　（b＞0）　とおける。

　これらを、ｙ＝ｘ²＋ａｘ　に代入してbを求めると、b=5/11（※）

b=1のとき、△PQR=(/4)(2)^2=5　なので、S₁=(5)(5/11)^2=375/121

# （※）は代入した2式からabの項を消去すると簡単に求まります。

S₂：　上から、Q(10/11，20/11)、R((5-30)/11，(10+15)/11)　で、放物線の式

　は、ｙ＝ｘ²＋((22-10)/11)x

　放物線とy=-x/2の原点以外の交点Sのx座標を求めると、x=(20√3-55)/22　なので、

　SP=-(20-55)/22・/2

　また、PQ=10/11・　なので、

　S₂={-(20-55)/22}{10/11}・5/4=125(11-12)/484

S₃：　放物線と　y-20√3/11=-(x-10√3/11)/2　のQ以外の交点Tのx座標を求めると、

　　x=-5/2　なので、　TQ=(5/2+10/11)・/2

　また、　PQ=10/11・　なので、

　S₃={5/2+10/11}{10/11}・5/4=125(11+12)/484


＃見た目は違いますが、GAIさんと同じ結果になりました。