このとき、 黄色の三角形の面積和と水色の三角形の面積和の比が、３：２となることは瞬時に了解されるだろう。
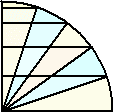
これが、もしも下図のように５等分点で平行線を引き５つの図形に分割した場合はどうだろう。
上記と同様に、黄色部分の面積和と水色部分の面積和の比が、３：２となるとは俄には信じられないだろう。
実際に、最上段の三角形の面積を１とすると、２段目の水色部分の面積は、４−１＝３
３段目の黄色部分の面積は、９−４＝５
４段目の水色部分の面積は、１６−９＝７
５段目の黄色部分の面積は、２５−１６＝９
以上から、黄色部分の面積和は、１＋５＋９＝１５
水色部分の面積和は、３＋７＝１０
なので、 黄色部分の面積和と水色部分の面積和の比は、３：２となる。
DD++さんからのコメントです。（令和元年１１月１２日付け）
同じ三角形を２つ用意して、片方を180°ひっくり返してくっつければ、直感的に納得できま
すね。
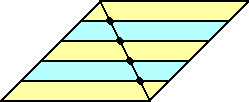
（コメント） なるほど！一目瞭然ですね。
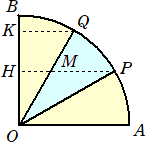
同様に、中心角が９０°の扇形に対して、中心角を５等分して５つの扇形に分割する。
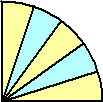このとき、 黄色の扇形の面積和と水色の扇形の面積和の比が、３：２となることは瞬時に了解されるだろう。
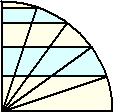
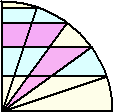
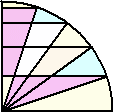
これが、もしも下図のように角の５等分点で平行線を引き５つの図形に分割した場合は
どうだろう。
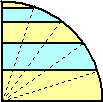上記と同様に、黄色部分の面積和と水色部分の面積和の比が、３：２となるとは俄には信じられないだろう。
実際に、頂角θ（＝１８°）、半径２の扇形の面積をＳとおくと、
最上段の図形の面積は、 Ｓ−ｓｉｎ２θ で、
２段目の水色部分の面積は、２Ｓ−（Ｓ−ｓｉｎ２θ）−ｓｉｎ４θ＝Ｓ＋ｓｉｎ２θ−ｓｉｎ４θ
３段目の黄色部分の面積は、
３Ｓ−（Ｓ−ｓｉｎ２θ）−（Ｓ＋ｓｉｎ２θ−ｓｉｎ４θ）−ｓｉｎ６θ＝Ｓ＋ｓｉｎ４θ−ｓｉｎ６θ
４段目の水色部分の面積は、
４Ｓ−（Ｓ−ｓｉｎ２θ）−（Ｓ＋ｓｉｎ２θ−ｓｉｎ４θ）−（Ｓ＋ｓｉｎ４θ−ｓｉｎ６θ）−ｓｉｎ８θ
＝Ｓ＋ｓｉｎ６θ−ｓｉｎ８θ
５段目の黄色部分の面積は、Ｓ＋ｓｉｎ８θ
以上から、黄色部分の面積和は、
Ｓ−ｓｉｎ２θ＋Ｓ＋ｓｉｎ４θ−ｓｉｎ６θ＋Ｓ＋ｓｉｎ８θ＝３Ｓ−ｓｉｎ２θ＋ｓｉｎ４θ−ｓｉｎ６θ＋ｓｉｎ８θ
水色部分の面積和は、
Ｓ＋ｓｉｎ２θ−ｓｉｎ４θ＋Ｓ＋ｓｉｎ６θ−ｓｉｎ８θ＝２Ｓ＋ｓｉｎ２θ−ｓｉｎ４θ＋ｓｉｎ６θ−ｓｉｎ８θ
ここで、
ｓｉｎ２θ−ｓｉｎ４θ＋ｓｉｎ６θ−ｓｉｎ８θ
＝ｓｉｎ６θ＋ｓｉｎ２θ−（ｓｉｎ８θ＋ｓｉｎ４θ）
＝２ｓｉｎ４θｃｏｓ２θ−２ｓｉｎ６θｃｏｓ２θ
＝−２ｃｏｓ２θ（ｓｉｎ６θ−ｓｉｎ４θ）
＝−４ｃｏｓ２θｃｏｓ５θｓｉｎθ
ここで、θ＝１８°なので、５θ＝９０° よって、ｃｏｓ５θ＝０
すなわち、 ｓｉｎ２θ−ｓｉｎ４θ＋ｓｉｎ６θ−ｓｉｎ８θ＝０ となる。（← 美しい！）
したがって、黄色部分の面積和は、３Ｓ、水色部分の面積和は、２Ｓ なので、
黄色部分の面積和と水色部分の面積和の比は、３：２となる。
（コメント） 扇形の場合、３：２になることは自信が持てませんでしたが、確かに計算すると、
３：２になるんですね！本当に驚きです。
なつさんからのコメントです。（令和元年１１月７日付け）
最後の[角の５等分点で平行線を引き５つの図形に分割した場合]の話は、わざわざ三角
関数を用いなくても面積が等しいことが示せそうです。
合同な直角三角形を2組考えて、直角三角形を移動していけば[中心角が９０°の扇形に
対して、中心角を５等分して５つの扇形に分割した場合]の状態と同じになりますね…。
記号を置いてあげないと上手く説明できないですが。
（コメント） なつさんのアイデアを「角の３等分点」の場合に適用してみました。
（令和元年１１月９日付け）
